NumXL Pro
NumXL es un conjunto complementos de series de Excel. Transforma su aplicación Microsoft® Excel® en una herramienta econométrica y de series de tiempo de primera. Una herramienta que ofrece la clase de exactitud estadística ofrecida por otros paquetes estadísticos mucho más costosos. NumXL se integra a la perfección con Excel, adicionando decenas de funciones econométricas, un rico conjunto de atajos y una interfaz de usuario intuitiva para guiarnos durante todo el proceso.
Ya sea que tengamos un simple problema con una tarea o un proyecto empresarial de gran escala, NumXL simplifica nuestros esfuerzos. Nos ayuda a conseguir nuestros objetivos de la forma más rápida y rigurosa posible.
NumXL también guarda nuestros datos y resultados conectados en Excel, permitiéndonos rastrear nuestros cálculos, adicionar nuevos puntos de datos, actualizar un análisis existente y compartir nuestros resultados con facilidad.
NumXL nos permite comenzar a ejecutar, no requiere ningún tipo de conocimiento en programación o codificación, y está diseñado para facilitar su uso; no tendremos que trasladar nuestros datos entre programas externos. También podemos realizar cualquier tipo de análisis ad hoc puesto que todas las funciones de NumXL están disponibles en nuestra hoja de cálculo y dentro del entorno de VBA en caso de que elijamos escribir macros.
¿Qué puede hacer NumXL por mí?
- Ubicación o tendencia central: media, mediana, tendencia, etc.
- Variabilidad o estadística de dispersión.
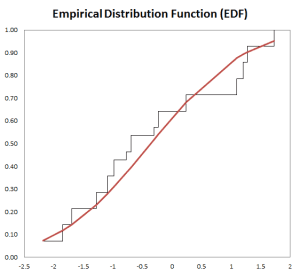
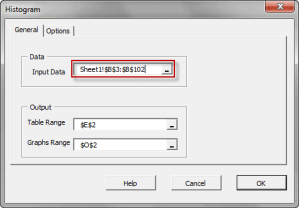
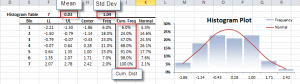
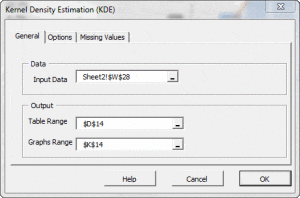
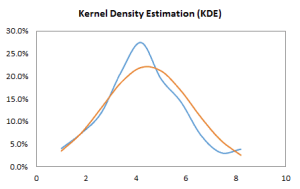
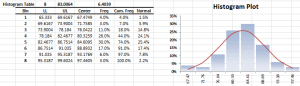
- Forma de distribución, ya sea vía índices tales como asimetría, kurtosis, centil, o vía formatos de tabulación y/o gráficos tales como histograma, EDF y Estimado de densidad de Kernel (KDE).
- Dependencia estadística: serial/auto-correlación y correlación cruzada.
Funciones destacadas:
| Función | Descripción |
|---|---|
| EWMA | Volatilidad Ponderada Exponencial |
| GINI | Coeficiente de GINI |
| Quantile | Cuantil de muestra |
| IQR | El Rango Intercuartílico (RIC) |
| MD | Diferencia absoluta Promedio |
| MAD | Desviación absoluta media |
| RMD | Diferencia Media Relativa |
| LRVar | Variación a largo plazo (Bartlett Kernel) |
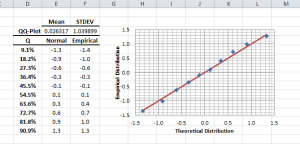
La variable de distribución está representada por una gráfica o tabulación.
Funciones destacadas:
| Función | Descripción |
|---|---|
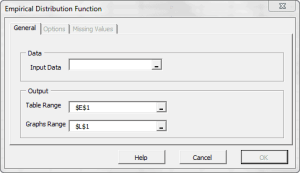
| EDF | Función de distribución empírica |
| KDE | Estimación de Densidad de Kernel |
| NxHistogram | (Histograma) de Distribución de Frecuancia |
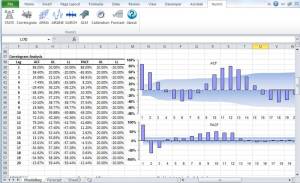
- Para un conjunto de datos las funciones de autocorrelación o seriales(ej.. ACF, PACF) son herramientas de uso común, no solamente para revisar lo aleatorio, sino también en etapas de identificación de modelos para tipos de modelo ARMA.
Funciones destacadas:Función Descripción ACF Función de Autocorrelación (FAC) PACF Autocorrelación Parcial Hurst El exponente de Hurst - Para dos o más variables, se usan correlaciones cruzadas para medir cómo esas variables se relacionan entre sí.
Funciones destacadasFunción Descripción XCF Función de correlación cruzada (FCC) EWXCF Correlación ponderada exponencial
Ver también
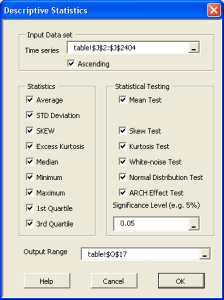
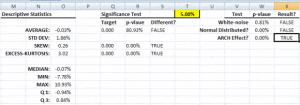
Hacer pruebas estadísticas o de hipótesis es un método común para dibujar inferencias sobre una población basada en evidencia estadística de una muestra. Por ejemplo, las pruebas estadísticas técnicas son aplicadas con frecuencia en el examen de significación (ej. Diferencia de cero) de un parámetro calculado (ej. Media, distorsión, curtosis), o para verificar la conjetura (ej. Normalidad, ruido blanco, estacionario, cointegración, multicolinealidad, etc.) usando datos de muestra finitos.
En NumXL, las funciones de prueba estadística pueden ser desagregadas en las siguientes categorías:
Esta categoría describe un conjunto de pruebas de una muestra que comparan: la media de una muestra (u otra medida de ubicación) con un estándar conocido (conocido en la teoría o que sea calculado sobre la población).
Funciones destacadas:
| Función | Descripción |
|---|---|
| TEST_MEAN | Prueba media de una muestra de población |
Estas también son pruebas de una muestra que comparan la varianza de una muestra (u otra medida de dispersión estadística) con un estándar conocido (conocido en la teoría pero que es calculado sobre la población).
Funciones destacadas:
| Función | Descripción |
|---|---|
| TEST_STDEV | Prueba de desviación estándar |
| TEST_SKEW | Prueba de Asimetria |
| TEST_XKURT | Prueba de Exceso de curtosis |
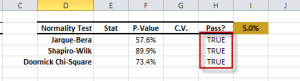
Las pruebas estadísticas son pruebas de una muestra que examinan la conjetura sobre la distribución de una variable aleatoria.
Funciones destacadas:
| Función | Descripción |
|---|---|
| NormalityTest | Pruebas para distribución normal o gaussiana |
- Una variable – correlación serial (aka Auto)
Funciones destacadas:
Función Descripción ACFTest Prueba de Autocorrelación WNTest Prueba de ruido blanco ARCHTest Prueba ARCH ADFTest Prueba estacionaria de Dickey Fuller Aumentada
- Una variable – correlación serial (aka Auto)
- Dos o más variables -correlación cruzada
Funciones destacadas:
Función Descripción XCFTest Prueba de Correlación Cruzada JohansenTest Prueba de Cointegración Johansen Chow Test Prueba de Estabilidad de Regresión CollinearityTest Prueba de Colinealidad/Multi-colinealidad
Ver también
La construcción de la curva puede involucrar interpolación donde se requiere un ajuste exacto a los datos, o suavizado; en el que se construye la función que se ajusta a los datos de manera aproximada.
Descubre una función que se ajusta exactamente a los puntos de datos. NumXL soporta una o dos interpolaciones dimensionales.
Funciones destacadas:
| Función | Descripción |
|---|---|
| NxINTRPL | Extrapolación e interpolación lineal, polinomial, spline cubica |
| NxINTRPL2D | 2- Extrapolación e interpolación dimensional |
Encuentra una función que se ajusta aproximadamente a los puntos de datos pero le damos espacio al error y permitimos que nuestros puntos estén cerca pero no necesariamente en la curva, dado que el error es minimizado en general.
Funciones destacadas:
| Función | Descripción |
|---|---|
| NxRegress | Regresión |
| NxKNN | K Barrios más cercanos (K-NN ) Regresión |
| NxKREG | Regresión de Kernel |
| NxLOCREG | Regression local movimiento polinomial |
Ver también
- Videos Tutoriales
- Manual de Referencia
- Guía de Usuario
- Notas Técnicas
- Consejos y Trucos
- Estudios de caso
Funciones destacadas:
| Función | Descripción |
|---|---|
| DIFF | Operador de Diferencias de Series Temporales |
| LAG | Rezago u operador de rezago |
| INTG | Operador integral de series de tiempo |
Funciones destacadas:
| Función | Descripción |
|---|---|
| BoxCox | Transformada de Box-Cox |
| CLOGLOG | Transformación Log-Log Complementaria |
| LOGIT | Transformación de logit |
| PROBIT | Transformación Probit |
| DETREND | Elimina tendencias |
Funciones destacadas:
| Función | Descripción |
|---|---|
| SUBNA | Valores faltantes interpolados |
Funciones destacadas:
| Función | Descripción |
|---|---|
| RESAMPLE | Series de tiempo de remuestreo |
Ver también
- Videos Tutoriales
- Manual de Referencia
- Guía de Usuario
- Notas Técnicas
- Consejos y Trucos
- Estudios de caso
Funciones destacadas:
| Función | Descripción |
|---|---|
| NxSort | Clasificación de un conjunto de datos |
| NxReverse | Reversa el orden cronológico |
| NxShuffle | Mezcla el orden de los elementos en el conjunto de datos |
Funciones destacadas:
| Función | Descripción |
|---|---|
| NxSubset | Subconjunto de series de tiempo |
| NxChoose | Muestreo Aleatorio |
Ver también
- Videos Tutoriales
- Manual de Referencia
- Guía de Usuario
- Notas Técnicas
- Consejos y Trucos
- Estudios de caso
Promedio ponderado móvil unilateral, centrado, simple o doble.
Funciones destacadas:
| Función | Descripción |
|---|---|
| NxEMA | Promedio exponencial móvil ponderado (en curso/corriendo) |
| NxMA | Promedio móvil (en curso) usando puntos de datos previos |
| WMA | Promedio móvil ponderado |
| NxCMA | Filtro promedio móvil centrado |
| NxSMA | Filtro estacional móvil promedio |
Optimizador incorporado para parámetros de suavizado y valor inicial.
Funciones destacadas:
| Función | Descripción |
|---|---|
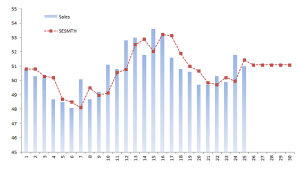
| SESMTH | Suavizado Exponencial Simple de Brown |
| LESMTH | Suavizado exponencial lineal de Brown |
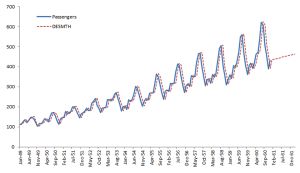
| DESMTH | Doble Suavizado Exponencial de Holt |
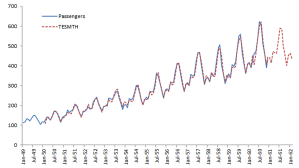
| TESMTH | Suavizado triple exponencial de Holt-Winters |
| GESMTH | Suavizado exponencial general |
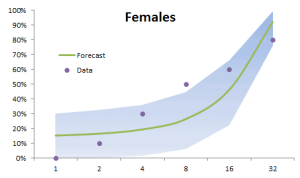
El análisis de tendencia se usa con mucha frecuencia en la industria (incluso se abusa) para hacer un pronóstico rápido (y turbio). Los ejecutivos podrán utilizar la herramienta de tendencia como una verificación de juicio cuando se examinen resultados para modelos más avanzados. NumXL soporta varias formas de tendencia: lineal, polinomial, poder, exponencial y logarítmico.
Funciones destacadas:
| Función | Descripción |
|---|---|
| NxTrend | Tendencia determinista en una serie de tiempo |
Ver también
- Videos Tutoriales
- Manual de Referencia
- Guía de Usuario
- Notas Técnicas
- Consejos y Trucos
- Estudios de caso
NumXL ofrece una amplia selección de modelos ARMA/ARIMA tales como ARMA (Promedio autorregresivo móvil), ARIMA (Promedio autorregresivo integrado móvil), SARIMA (Promedio autorregresivo estacional integrado móvil), ARMAX (Promedio autorregresivo móvil con variables exógenas), SARIMAX, y ARIMA X12 para el Censo EEUU.
Por definición, el promedio autorregresivo móvil (ARMA) es un proceso estacionario estocástico hecho con sumas de componentes autorregresivos y de promedio móvil:
Donde:
- $x_t$ es el resultado observado en un tiempo t.
- $a_t$ es la innovación, el shock o término de error en un tiempo t.
- $p$ es el orden de las últimas variables retrasadas.
- $q$ es el orden de la última innovación retrasada o shock.
- $a_t$ Las observaciones de una serie de tiempo _t son independientes e idénticamente distribuidas
(i.e. i.i.d) y siguen una distribución gaussiana
(i.e. $\Phi(0,\sigma^2)$).
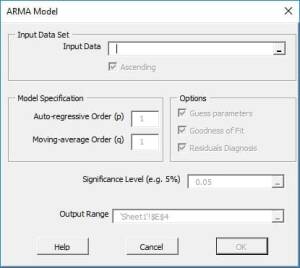
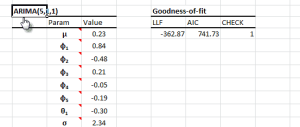
Funciones destacadas:
| Función | Descripción |
|---|---|
| ARMA | Definición de un modelo ARMA |
| ARMA_CHECK | Compruebe los valores de los parámetros para la estabilidad del modelo |
| ARMA_PARAM | Valores de los parámetros del modelo |
| ARMA_GOF | Valores de los parámetros del modelo |
| ARMA_FIT | Modelo ARMA Valores Ajustados |
| ARMA_FORE | Pronóstico del modelo ARMA |
| ARMA_SIM | Valores simulados de un modelo ARMA |
Por definición, el promedio autorregresivo móvil (ARMA) es un proceso estacionario estocástico hecho de sumas de componentes autorregresivos o de promedio móvil:
\[ y_t = (1-L)^d x_t \]
Donde:
- $x_t$ es la salida original no estacional en el momento t.
- $y_t$ es la salilda diferenciada (estacional) observada en el momento t.
- $d$ es el orden de integración de la series de tiempo.
- $a_t$ es el cambio o innovation, choque o término de error en el tiempo t.
- $p$ es el orden de la última variable rezagada (lagged).
- $q$ es el orden del último cambio de rezago o choque.
- $a_t$ las observaciones de las series de tiempo son independientes e idénticamente distribuídas (es decir, i.i.d) y siguen una distribución Gaussianna (es decir, $\Phi(0,\sigma^2)$)
Funciones destacadas:
| Función | Descripción |
|---|---|
| ARIMA | Definición de un modelo ARIMA |
| ARIMA_CHECK | Comprueba los valores de los parámetros para la estabilidad del modelo |
| ARIMA_PARAM | Valores de los parámetros del modelo |
| ARIMA_GOF | Calidad de ajuste de un modelo ARIMA |
| ARIMA_FIT | Modelo ARIMA Valores Ajustados |
| ARIMA_FORE | Pronóstico del modelo ARIMA |
| ARIMA_SIM | Valores Simulados de un Modelo ARIMA |
El modelo SARIMA es la extensión del modelo ARIMA, usado con frecuencia cuando sospechamos que un modelo puede tener un efecto estacional.
Por definición, el proceso del promedio estacional autorregresivo integrado móvil SARIMA (p,d,q)(P,D,Q)s – es la multiplicación de dos procesos ARMA de series de tiempo diferenciadas.
(1-L^s)^D x_t = \\ (1+\sum_{i=1}^q {\theta_i L^i})(1+\sum_{j=1}^Q {\Theta_j L^{j
\times s}}) a_t \]
\[ y_t = (1-L)^d (1-L^s)^D \]
Donde:
- $x_t$ es la salida original no estacional en el tiempo t.
- $y_y$ es la salida diferenciada (estacional) en el tiempo t.
- $d$ es el orden de integración no estacional de las series temporales.
- $p$es el orden del componente AR no estacional.
- $P$ es el orden del componente AR no estacional.
- $q$ es el orden del componente MA no estacional.
- $Q$ es el orden del componente MA estacional.
- $s$ es la duración estacional.
- $D$ es el orden de integración de las series de tiempo esatcionales.
- $a_t$ es la innovación, choque o término de error en el tiempo t.
- $\{a_t\}$ las observaciones de series de tiempo son independientes e idénticamente distribuidas (es ecir i.i.d) y siguen una distribución de Gauss. (i.e. $\Phi(0,\sigma^2)$)
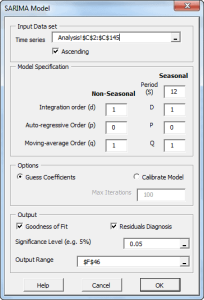
Funciones destacadas:
| Función | Descripción |
|---|---|
| SARIMA | Definición del Modelo SARIMA |
| SARIMA_CHECK | Validación del Modelo SARIMA |
| SARIMA_PARAM | Parámetros del modelo SARIMA |
| SARIMA_GOF | Bondad de ajuste SARIMA |
| SARIMA_FIT | Ajuste en la muestra SARIMA |
| SARIMA_FORE | Función de pronóstico SARIMA |
| SARIMA_SIM | Modelado Basado en Simulación SARIMA |
El modelo de aerolínea es un caso especial -pero usado con frecuencia, de modelos multiplicativos ARIMA. Para una longitud (s) estacional dada, el modelo de aerolínea se define por 4 parámetros: $\mu$, $\sigma$, $\theta$ and $\Theta$).
\[ Z_t = (1-L^s)(1-L)Y_t = \mu + (1-\theta L)(1-\Theta L^s)a_t \] O
\[ Z_t = \mu -\theta \times a_{t-1}-\Theta \times a_{t-s} +\theta\times\Theta \times a_{t-s-1}+ a_t \]
Donde:
- $s$ es la longitud de la estacionalidad.
- $\mu$ es la media del modelo.
- $\theta$ es el coeficiente del primer cambio del rezago.
- $\Theta$ es el coeficiente del cambio del rezago standard.
- $\left [a_t\right ] $ son los cambios o innovaciones de las series de tiempo.
Funciones destacadas:
| Función | Descripción |
|---|---|
| AIRLINE_CHECK | Compruebe los valores de los parámetros para la estabilidad del modelo |
| AIRLINE_PARAM | Valores de los parámetros del modelo |
| AIRLINE_GOF | Calidad de ajuste de un modelo Airline |
| AIRLINE_FIT | Modelo Airline Valores Ajustados |
| AIRLINE_FORE | Pronóstico del modelo Airline |
| AIRLINE_SIM | Valores simulados de un modelo Airline |
En principio, un modelo ARMAX es un modelo de regresión lineal que usa un proceso de tipo ARMA (i.e. wt) para modelar residuos:
\[ (1-\phi_1 L – \phi_2L^2-\cdots-\phi_pL^p)(y_t-\alpha_o -\beta_1 x_{1,t} – \beta_2 x_{2,t} – \cdots – \beta_b x_{b,t})= (1+ \theta_1 L + \theta_2 L^2 + \cdots + \theta_q L^q)a_t \]
\[ (1-\phi_1 L – \phi_2 L^2 – \cdots – \phi_p L^p)w_t= (1+\theta_1 L+ \theta_2 L^2 + \cdots + \theta_q L^q ) a_t \]
\[ a_t \sim \textrm{i.i.d} \sim \Phi (0,\sigma^2) \]
Donde
- $L$ es el operador de rezago (también conocido como back-shift).
- $y_t$ es la salida observada en el tiempo t.
- $x_{k,t}$ es la variable k-ésima en el tiempo t.
- $\beta_k$ es el valor del coeficiente para la k-ésima variable de entrada explicativa.
- $b$ es el número de variables de entrada exógenas.
- $w_t$ son los residuales de regresión autocorrelacinados.
- $p$ es el orden de las últimas variables rezagadas.
- $q$ es el orden del último cambio rezagado o choque.
- $a_t$ es el cambio (innovation), choque o terminos de error en el tiempo t.
- $a_t$ observaciones de series de tiempo son independientes e idénticamente distribuidas (es decir, i.i.d) y seguidas de una distribución Gaussian (es decir. $\Phi(0,\sigma^2)$)
Funciones destacadas:
| Función | Descripción |
|---|---|
| ARMAX | Definición de un modelo ARMAX |
| ARMAX_CHECK | Compruebe los valores de los parámetros para la estabilidad del modelo |
| ARMAX_PARAM | Valores de los parámetros del modelo |
| ARMAX_GOF | Calidad de ajuste de un modelo ARMAX |
| ARMAX_FIT | Modelo ARMAX Valores Ajustados |
| ARMAX_FORE | Pronóstico para el modelo ARMAX |
| ARMAX_SIM | Modelo de simulación ARMAX |
En principio, un modelo SARIMAX es un modelo de regresión lineal que usa un proceso tipo SARIMA (i.e.) Este modelo es útil en casos en los que sospechamos que pueden existir residuos en una tendencia o patrón estacional.
\[ (1-\sum_{i=1}^p {\phi_i L^i})(1-\sum_{j=1}^P {\Phi_j L^{j \times s}})(1-L)^d (1-L^s)^D w_t -\eta = (1+\sum_{i=1}^q {\theta_i L^i})(1+\sum_{j=1}^Q {\Theta_j L^{j \times s}}) a_t \]
Donde:
- $L$ es el operador de rezago (mejor conocido como back-shift).
- $y_t$ es la salida observada en el tiempo t.
- $x_{k,t}$ es la variable de entrada exógena k-ésimo en el tiempo t.
- $\beta_k$ es el valor del coeficiente de la variable de entrada k-ésima exógena (explicativa).
- $b$ el el número de variables de entradas exógenas.
- $w_t$ son los residuos de la regresión de auto-correlación.
- $p$ es el orden del componente AR no estacional.
- $P$ es el orden del componente RA estacional.
- $q$ es el orden del componente MA no estacional.
- $Q$ es el orden del componente estacional MA.
- $s$ es la duración de la estacionalidad.
- $D$ es el orden de integración de estacionalidad de la series de tiempo.
- $\eta$ es una constante en el modelo SARIMA.
- $a_t$ es la innovación, shock o término de error en el tiempo t.
- $\{a_t\}$ las observaciones de series de tiempo son independientes e idénticamente distribuidos (es decir i.i.d) y siguen una distribución de Gauss (i.e. $\Phi(0,\sigma^2)$).
Funciones destacadas:
| Función | Descripción |
|---|---|
| SARIMAX | Definición de un modelo SARIMAX |
| SARIMAX_PARAM | Parámetros del modelo SARIMA |
| SARIMAX_CHECK | Validación del modelo SARIMAX |
| SARIMAX_GOF | Bondad de ajuste SARIMAX |
| SARIMAX_FIT | Valores ajustados en la muestra SARIMAX |
| SARIMAX_FORE | Pronósticos basados en SARIMAX |
| SARIMAX_SIM | Simulación basada en modelos SARIMAX |
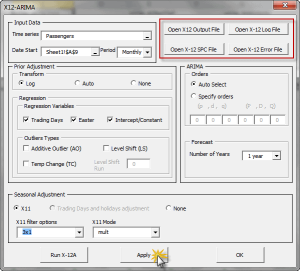
El software X-12-ARIMA viene con extensas series de tiempo de modelado y capacidades de modelado de selección para modelos de regresión lineal con errores ARIMA (modelos regARIMA).
Los modelos ARIMA, como lo discutieron Box y Jenkins (1976), son usados frecuentemente para series de tiempo estacionales. Un modelo general multiplicativo estacional ARIMA para una serie de tiempo z_t se puede escribir:
Donde:
- $L$ es el rezago del operador Backshift.
- $s$ es el periodo estacional.
- $(\phi(L)=\phi_o+\phi_1 L+\phi_2 L^2 +\cdots +\phi_p L^p)$ es el modelo del componente no estacional autorregresivo (AR).
- $(\Phi(L)=\Phi_o+\Phi_1 L+\Phi_2 L^2 +\cdots +\Phi_P L^P)$ es el modelo del componente estacional autorregresivo (AR).
- $(\theta(L)=\theta_o+\theta_1 L+\theta_2 L^2 +\cdots +\theta_q L^q)$
es el promedio móvil no estacional del modelo componente (MA). - $(\Theta(L)=\Theta_o+\Theta_1 L+\Theta_2 L^2 +\cdots +\Theta_Q L^Q)$
es el promedio móvil (MA) estacional del modelo componente. - $(1-L)^d$ es el operador de diferenciación no estacional de orden d.
- $(1-L)^D$ es el operador de diferenciación estacional de orden D y período (s) estacional.
- $\{a_t\}\sim \textrm{i.i.d}\sim N(0,\sigma^2)$
Funciones destacadas:
| Función | Descripción |
|---|---|
| X12ARIMA | Definición de un modelo X12-ARIMA |
| X12APROP | X11 Ajuste estacional y propiedades del modelo X12-ARIMA |
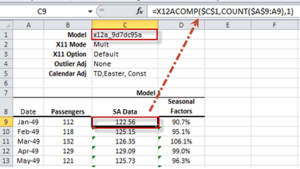
| X12ACOMP | Series de tiempo de salida X12-ARIMA |
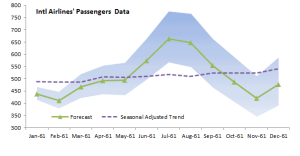
| X12AFORE | Pronóstico para el modelo X12-ARIMA |
El software X-13ARIMA-SEATS viene con extensas series de tiempo de modelado y capacidades de modelado de selección para modelos de regresión lineal con errores ARIMA (modelos regARIMA).
Además, el X-13ARIMA-SEATS incluye la capacidad de generar un ajuste estacional basado en el modelo ARIMA utilizando una versión del software SEATS desarrollado originalmente por Víctor Gómez y Agustín Maravall en el Banco de España, así como ajustes no paramétricos del procedimiento X-11.
Funciones destacadas:
| Función | Descripción |
|---|---|
| X13AS | Definición de un modelo X-13ARIMA-SEATS |
| X13ASCOMP | Series de tiempo de salida X-13ARIMA-SEATS |
| X13ASFORE | Pronóstico para el modelo X-13ARIMA-SEATS |
Ver también
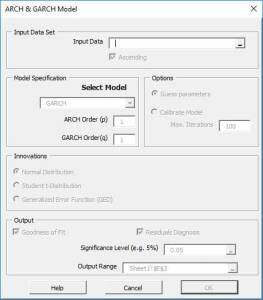
Los modelos ARCH son comúnmente empleados en el modelado de series de tiempo financieras que exhiben volatilidad de tiempo variado y volatilidad acumulada, ej. períodos de vaivenes intercalados con períodos de relativa calma. Los modelos de tipo ARCH son a veces considerados parte de la familia de los modelos de volatilidad estocástica, aunque esto es estrictamente incorrecto desde que en el tiempo t la volatilidad es completamente pre determinada (determinista) si se dan valores previos.
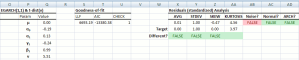
Igual que en el caso de ARMA/ARIMA, modelar un modelo tipo GARCH es muy fácil. Usando la herramienta GARCH podemos generar una tabla de modelo de resultado con todos los valores de coeficiente y cálculos relacionados (ej. LLF y diagnóstico residual). Esta tabla puede ser usada para calibrar el modelo y predecir valores fuera de la muestra.
Si un modelo promedio autorregresivo móvil (modelo ARMA) se asume como error de varianza, el modelo es un modelo de heterocedasticidad condicional autorregresiva generalizada (GARCH, Bollerslev(1986)).
\[ \sigma_t^2 = \alpha_o + \sum_{i=1}^p {\alpha_i a_{t-i}^2}+\sum_{j=1}^q{\beta_j \sigma_{t-j}^2} \]
\[ a_t = \sigma_t \times \epsilon_t \]
\[ \epsilon_t \sim P_{\nu}(0,1) \]
Donde:
- $x_t$ es el valor de las series de timepo en el tiempo t.
- $\mu$ es la media del modelo GARCH.
- $a_t$ es residual del modelo en el tiempo t.
- $\sigma_t$ es la desviación estándar condicional (es decir, la volatilidad) en el tiempo t.
- $p$ es el orden del modelo de componentes ARCH.
- $\alpha_o,\alpha_1,\alpha_2,…,\alpha_p$ son los parámetros de la el modelo de componente ARCH.
- $q$ es el orden del modelo de componente GARCH.
- $\beta_1,\beta_2,…,\beta_q$ son los parámetros del modelo de componente GARCH.
- $\left[\epsilon_t\right]$ son los residuos estandarizados:
$\left[\epsilon_t\right] \sim i.i.d$
$E\left[\epsilon_t\right]=0$
$\mathit{VAR}\left[\epsilon_t\right]=1$ - $P_{\nu}$ es la función de distribución de probabilidad para$\epsilon_t$.
En la actualidad, son compatibles las siguientes distribuciones:- Distribución Normal
$P_{\nu} = N(0,1) $. - Distribución t de Student
$P_{\nu} = t_{\nu}(0,1) $
$\nu \succ 4 $ - Distribución de error generalizado (GED)
$P_{\nu} = \mathit{GED}_{\nu}(0,1) $
$\nu \succ 1 $
- Distribución Normal
Funciones destacadas:
| Función | Descripción |
|---|---|
| GARCH | Definición de un modelo GARCH |
| GARCH_GUESS | Valores Iniciales de los parámetros GARCH |
| GARCH_CHECK | Verificar los valores de los parámetros para la estabilidad del modelo |
| GARCH_LLF | Función Log-Probabilidad GARCH |
| GARCH_RESID | Residuales GARCH |
| GARCH_FORE | Modelo de Pronóstico para el modelo GARCH |
| GARCH_SIM | simulación basada en GARCH |
| GARCH_VL | Volatilidad a largo plazo GARCH |
La heterocedasticidad condicional autorregresiva general exponencial (EGARCH) es otra forma del modelo GARCH. El modelo E-GARCH fue propuesto por Nelson (1991) para superar las debilidades de series de tiempo financieras en el manejo GARCH. En particular, para permitir los efectos asimétricos entre los rendimientos de activos positivos y negativos:
\[ \ln\sigma_t^2 = \alpha_o + \sum_{i=1}^p {\alpha_i \left(\left|\epsilon_{t-i}\right|+\gamma_i\epsilon_{t-i}\right )}+\sum_{j=1}^q{\beta_j \ln\sigma_{t-j}^2} \]
\[ a_t = \sigma_t \times \epsilon_t \]
\[ \epsilon_t \sim P_{\nu}(0,1) \]
Donde:
- $x_t$ es el valor de las series de tiemoi en el tiempo t.
- $\mu$ es la media del modelo GARCH.
- $a_t$ es el modelo residual en el tiempo t.
- $\sigma_t$ es la desviación estándar condicional (es decir, volatilidad) en el tiempo t.
- $p$ es el orden del componente del modelo ARCH.
- $\alpha_o,\alpha_1,\alpha_2,…,\alpha_p$ son los parámetros del modelo de componente ARCH.
- $q$ es el orden del modelo de componente GARCH.
- $\beta_1,\beta_2,…,\beta_q$ son los parámetros del modelo de componente GARCH.
- $\left[\epsilon_t\right]$ son los residuos estandarizados:
$ \left[\epsilon_t \right] \sim i.i.d$
$ E\left[\epsilon_t\right]=0$
$ \mathit{VAR}\left[\epsilon_t\right]=1$ - $P_{\nu}$ es la función de distribución de probabilidad para $\epsilon_t$.
En la actualidad, las siguientes distribuciones son compatibles:- Distribución Normal
$P_{\nu} = N(0,1) $ - Distribución t de Student
$P_{\nu} = t_{\nu}(0,1) $
$\nu \gt 4 $ - Distribución de Error Generalizado (GED)
$P_{\nu} = \mathit{GED}_{\nu}(0,1) $
$\nu \gt 1 $
- Distribución Normal
Funciones destacadas:
| Función | Descripción |
|---|---|
| EGARCH | Definición de un modelo EGARCH |
| EGARCH_GUESS | Valores iniciales de los parámetros del modelo |
| EGARCH_CHECK | Compruebe los valores de los parámetros para la estabilidad del modelo |
| EGARCH_LLF | Función de verosimilitud de registro de un modelo de EGARCH |
| EGARCH_RESID | EGARCH ajusta los valores de los residuos estandarizados |
| EGARCH_FORE | Pronóstico del modelo EGARCH |
| EGARCH_SIM | Simulated values of a EGARCH Model |
| EGARCH_VL | Long-run Volatility of the EGARCH Model |
En finanzas el rendimiento de un valor puede depender de su volatilidad (riesgo). Para modelar tal fenómeno, el modelo GARCH en la media (GARCH-M) agrega un término de heterocedasticidad en la ecuación media. Tiene la siguiente especificación:
El modelo GARCH-M(p,q) está escrito así:
\[ x_t = \mu + \lambda \sigma_t + a_t \]
\[\sigma_t^2 = \alpha_o + \sum_{i=1}^p {\alpha_i a_{t- i}^2}+\sum_{j=1}^q{\beta_j \sigma_{t-j}^2} \]
\[ a_t = \sigma_t \times \epsilon_t \]
\[ \epsilon_t \sim P_{\nu}(0,1) \]
Donde:
- $x_t$ El modelo GARCH-M(p,q) está escrito así:
- $\mu$ es la media del modelo GARCH.
- $\lambda$ es el coeficiente de volatilidad para la media.
- $a_t$ es residual del modelo en el tiempo t.
- $\sigma_t$ es la desviación estándar condicional (es decir, la volatilidad) en el tiempo t.
- $p$ es el orden del modelo de componente ARCH.
- $\alpha_o,\alpha_1,\alpha_2,…,\alpha_p$ son los parámetros del modelo de componentes ARCH.
- $q$ es el fin del modelo de componentes GARCH.
- $\beta_1,\beta_2,…,\beta_q$ son los parámetros del modelo de componentes GARCH.
- $\left[\epsilon_t\right]$ son los residuos estandarizados:
$ \left[\epsilon_t \right]\sim i.i.d$
$ E\left[\epsilon_t\right]=0$
$ \mathit{VAR}\left[\epsilon_t\right]=1$ - $P_{\nu}$ es la función de distribución de probabilidad para $\epsilon_t$.
En la actualidad, son compatibles las siguientes distribuciones:- Distribución Normal
$P_{\nu} = N(0,1) $ - Distribución t de Student’s
$P_{\nu} = t_{\nu}(0,1) $
$\nu \gt 4 $ - Distribución de Error Generalizado (GED)
$P_{\nu} = \mathit{GED}_{\nu}(0,1) $
$\nu \gt 1 $
- Distribución Normal
Funciones destacadas:
| Función | Descripción |
|---|---|
| GARCHM | Definición de un modelo GARCH-M |
| GARCHM_GUESS | Parámetros Valores iniciales GARCHM |
| GARCHM_CHECK | Examina los parámetros del modelo para la estabilidad |
| GARCHM_LLF | Función de log-verosimilitud GARCHM |
| GARCHM_RESID | Residuales GARCHM |
| GARCHM_FORE | Pronóstico GARCHM |
| GARCHM_SIM | Simulacion Basada en GARCH-M |
| GARCHM_VL | Volatilidad de largo plazo GARCH-M |
Ver también
Un supuesto fundamental en los métodos econométricos es que las observaciones en series de tiempo están igualmente espaciadas y presentes. Esto surge porque las observaciones están hechas de manera deliberada a intervalos pares (procesos continuos) o porque el proceso sólo genera resultados en dicho intervalo de tiempo (proceso discreto).
Por ejemplo, una serie de tiempo financiera diaria de las acciones de IBM cerrando precios se basa en el calendario de vacaciones de NYSE, de manera que cada observación es tomada en un día de actividad comercial en NYSE (apertura/cierre). Para series de tiempo semanales o mensuales, el número de días comerciales varía de una observación a otra y de pronto debamos ajustarnos a su efecto.
Los eventos del calendario influencian los valores de las muestras de series de tiempo, y un ajuste previo de esos eventos nos ayudará a entender el proceso; modelando y haciendo pronósticos.
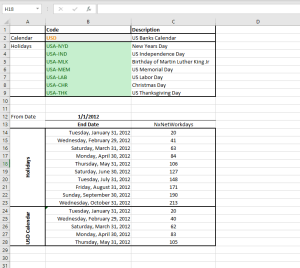
NumXL trae numerosas funciones para respaldar el ajuste del calendario, el ajuste de fecha escalonada, soporte de vacaciones en Estados Unidos y fuera de Estados Unidos, fines de semana no occidentales y calendarios públicos y de vacaciones en los bancos.
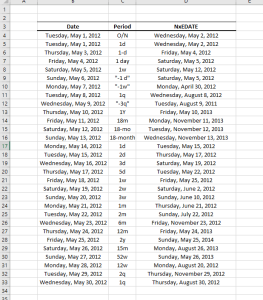
Estas funciones de cálculo de fecha le permitirán realizar cálculos con fechas y periodos como:
- Sumar y restar periodos en días, meses y años
- Mover una fecha dada al día laboral más cercano usando cualquiera de los días hábiles de la industria contando convenciones.
- Calcular la fecha del enésimo día de la semana dado (ej. El tercer viernes) en un mes determinado.
- Más
Funciones destacadas:
| Función | Descripción |
|---|---|
| NxAdjust | Mover hacia el día laboral más cercano |
| NxEDATE | Adelantar una fecha en un periodo de tiempo determinado |
| NxNetWorkdays | Número de días laborales en un rango de datos determinado |
| NxNWKDY | Día de la enésima semana en un mes |
| NxWKDYOrder | Orden del día de la semana para una fecha determinada |
| NxWorkday | Adelantar una fecha determinada N días laborales |
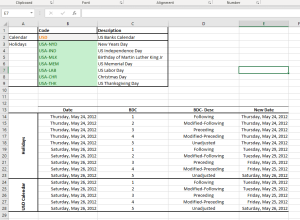
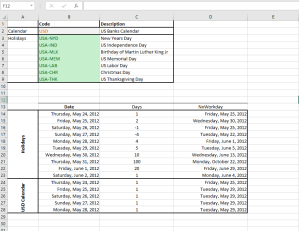
Un feriado es un día designado a tener un significado especial para los individuos, gobiernos o grupos religiosos. Típicamente, los feriados no necesariamente excluyen los días hábiles pero para nuestros propósitos, NumXL asume que todos los feriados admitidas (ej. Vacaciones nacionales) excluyen el trabajo normal.
Los feriados observados y las fechas actuales para los días de fiesta particulares (ej. Pascua) pueden variar según el país, de manera que en NumXL el código de feriados tiene como prefijo el código ISO del país (ej. USA, CAN, GBR, etc.)
Funciones destacadas:
| Función | Descripción |
|---|---|
| NxIsHoliday | Examina si una fecha determinada cae en feriado |
| NxFindHLDY | Busca el nombre del feriado que cae en una fecha determinada |
| NxHLDYDate | Calcula la fecha de un feriado determinado en un año dado |
| NxHLDYDates | Busca y devuelve todas las fechas de vacaciones en un rango de fecha determinado. |
Hasta Excel 2007, Microsoft soporta diferentes acontecimientos de fin de semana en la versión internacional de las funciones de datos (ej. WORKDAY.INTL). Las convenciones de fin de semana se definen o por un número o por un código de 7 dígitos.
Funciones destacadas:
| Función | Descripción |
|---|---|
| NxWKNDStr | Código de fin de semana |
| NxWKNDUR | Duración del fin de semana |
| NxWKNDate | Fecha del último y próximo fin de semana |
| NxWKNDNo | Número convencional de fin de semana |
| NxIsWeekend | Examina una fecha dada si cae en fin de semana. |
Para el análisis de tiempo financiero, un calendario es básicamente una definición de una lista de vacaciones observadas y una convención de días de fin de semana.
Los calendarios son extensamente usados al calcular funciones de fechas. NumXL viene con un número predefinido de calendarios (ej. Vacaciones del gobierno federal de EEUU, vacaciones de los Bancos en EEUU, calendario de los bancos en EEUU, etc.) pero los usuarios también pueden definir un calendario personalizado especificando vacaciones admitidas y convenciones semanales.
Featured Functions:
| Función | Descripción |
|---|---|
| NxCalendars | Devuelve una lista de calendarios de apoyo con un prefijo dado (opcional) |
| NxCALHolidays | Devuelve una lista de feriados admitidos en un determinado calendario |
| NxCALWKND | Devuelve la convención de fin de semana para un determinado calendario |
Ver también
- Videos Tutoriales
- Manual de Referencia
- Guía de Usuario
- Notas Técnicas
- Consejos y Trucos
- Estudios de caso
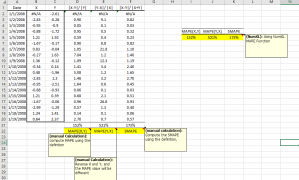
El pronóstico es un proceso en curso emprendido por varios accionistas para mejorar la exactitud y credibilidad en el tiempo.Hay numerosos métodos de pronóstico (cuantitativos, cualitativos y una mezcla de ambos) que pueden ser empleados, de manera que es imperativo para el proceso de pronostico ser monitoreado de manera efectiva, así la exactitud del pronóstico (o error) debe ser cuantificada con el tiempo.
Además, al cuantificar la exactitud del pronóstico con el tiempo, se puede usar para comparar muchos métodos de pronóstico.
Funciones destacadas:
| Función | Descripción |
|---|---|
| SSE | Sumatoria de errores cuadráticos |
| MSE | Media de errores cuadráticos |
| GMSE | Errores cuadráticos de media geométrica |
| SAE | Sumatoria de errores absolutos |
| MAE | Media de errores absolutos |
| RMSE | Raíz cuadrada del error cuadrático |
| GRMSE | Raíz cuadrada geométrica del error cuadrático medio |
Funciones destacadas:
| Función | Descripción |
|---|---|
| MAPE | Porcentaje de error de media absoluta |
| MdAPE | Porcentaje de error de mediana absoluta |
| MAAPE | Porcentaje de error de arcotangente media absoluta |
En esta categoría usamos el error de pronóstico relativo para un pronóstico estándar, tal como el del último valor disponible (Pronóstico Naïve 1), o el último valor disponible luego de la estacionalidad tiene que ser tomado en cuenta (Pronóstico Naïve 2).
Funciones destacadas:
| Función | Descripción |
|---|---|
| MRAE | Error absoluto de media relativa |
| MdRAE | Error absoluto de mediana relativa |
| GMRAE | Error absoluto de media relativa geometrica |
| MASE | Error escalado de media absoluta |
| PB | Mejor porcentaje |
| MDA | Exactitud de mediana direccional |
Ver también
- Videos Tutoriales
- Manual de Referencia
- Guía de Usuario
- Notas Técnicas
- Consejos y Trucos
- Estudios de caso
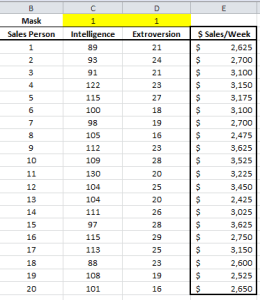
El análisis del factor es una herramienta útil para describir la variabilidad entre variables observadas y correlacionadas; en términos de un número potencialmente menor de variables no observadas y no correlacionadas llamadas factores.
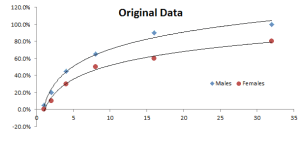
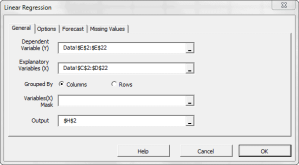
En estadística, la regresión lineal simple es el estimador de mínimos cuadráticos de un modelo lineal de regresión con una sola variable explicativa. En otras palabras; una regresión lineal simple ajusta una línea recta a través de un conjunto n de puntos, de tal manera que hace que la sumatoria de residuos cuadráticos del modelo (esto es: distancias verticales entre puntos del conjunto de datos y la línea de ajuste) sea tan pequeña como es posible.
Para el SLR, el objetivo es encontrar una línea recta que proporcione lo que mejor se ajusta a los puntos de datos ($x_i$,$y_i$) \[ y = \alpha + \beta \times x \]
Donde:
- $\alpha$ es la constante (aka interceptación) de la regresión.
- $\beta$ es el coeficiente (aka inclinación) de la variable explicativa.
Funciones destacadas:
| Función | Descripción |
|---|---|
| SLR_PARAM | Los valores del coeficiente para el modelo SLR |
| SLR_GOF | Bondad de ajuste (R^2, LLF, AIC) para el modelo SLR |
| SLR_FITTED | Valores ajustados (media y residuos) del modelo SLR |
| SLR_FORE | Pronóstico (de media y error) del modelo SLR |
| SLR_SNOVA | Análisis de la varianza del modelo SLR |
Dado un conjunto de datos $\{y_i,\, x_{i1}, \ldots, x_{ip}\}_{i=1}^n$ de n unidades estadísticas, un modelo de regresión lineal asume que la relación entre la variable dependiente $\{y_i\}$ y el vector p del regresor $\{x_i\}$ es lineal. Esta relación es modelada a través de un término de interrupción o error variable $\{\epsilon_i\}$ — una variable aleatoria no observada que le suma ruido a la relación lineal entre la variable dependiente y los regresores.
El MLR se describe así: \[ y_i = \beta_1 x_{i1} + \cdots + \beta_p x_{ip} + \varepsilon_i \]
Donde:
- $\mathbf{x}^{\rm T}_i$ Es la matriz transpuesta
- $ i = 1, \ldots, n$
Funciones destacadas:
| Función | Descripción |
|---|---|
| MLR_PARAM | Valores de coeficiente del modelo MLR |
| MLR_GOF | Bondad de ajuste del modelo MLR |
| MLR_FITTED | Valores ajustados (de media y residuales) del modelo MLR |
| MLR_FORE | Pronóstico (de media, error, C.I) para el modelo MLR |
| MLR_ANOVA | Análisis de varianza para el modelo MLR |
| MLR_PRTest | Prueba parcial F de variables de regresión |
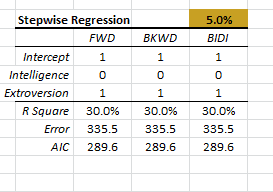
| MLR_STEPWISE | Método de selección de variables de regresión |
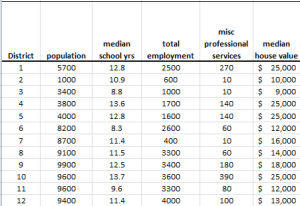
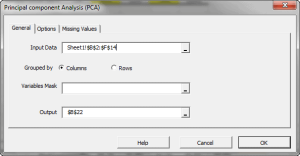
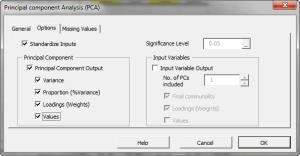
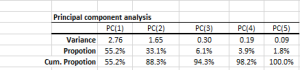
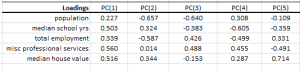
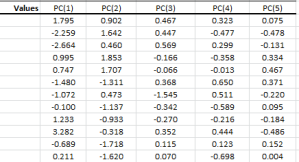
El análisis de Componente Principal (PCA) es un procedimiento matemático que usa una transformación lineal ortogonal para convertir un conjunto de observaciones de variables, posiblemente correlacionadas, en un conjunto de valores de variables no correlacionadas linealmente, llamado componente principal.
Además, cada columna (variable) tiene una media empírica de cero (la media empírica (de muestra) de la distribución ha sido restada del conjunto de datos).
La transformación PCA que preserva dimensionalidad Y (lo que quiere decir que le da el mismo número de componentes principales como variables originales) está dada por: \[ \mathbf{Y}^{\rm T} = \mathbf{X}^{\rm T}\mathbf{W} \]
Utilizando descomposición valor singulares (SVD) para el $ \mathbf{X}^{\rm T}$, podemos expresar la transformación PCA como \[ \mathbf{Y}^{\rm T} = (\mathbf{W}\mathbf{\Sigma}\mathbf{V}^{\rm T})^{\rm T}\mathbf{W} \]
Donde:
- $\mathbf{W}$ es la matriz de vectores propios de la matriz de covarianza $\mathbf{X} \mathbf{X}^{\rm T}$
- $\mathbf{V}$ es la matriz de vectores propios de la matriz the matrix $\mathbf{X}^{\rm T} \mathbf{X}$
- $\mathbf{\Sigma}$ es una matriz rectangular con números verdaderos no negativos en la diagonal
La transformación PCA $\mathbf{Y}$ es dada por: $ \mathbf{Y}^{\rm T} = \mathbf{V}\mathbf{\Sigma}^{\rm T} $
Funciones destacadas:
| Función | Descripción |
|---|---|
| PCA_COMP | Valores del componente principal (PC) |
| PCA_VAR | Calcula los valores de la variable usando un subconjunto de componentes principales |
El principal componente de regresión (PCR) es un procedimiento de dos etapas; primero se reduce el indicador de variables usando el análisis del componente principal, y luego se usan las variables reducidas en una regresión ajustada OLS.
PCR es usado con frecuencia cuando el número de variables predecido es grande, o cuando existen fuertes correlaciones entre las variables indicadas.
Funciones destacadas:
| Función | Descripción |
|---|---|
| PCR_PARAM | Calcula los valores de los coeficientes (y errores estándar) para el modelo PCR |
| PCR_GOF | Calcula la bondad de ajuste (e.g. $R^2$, LLF, AIC) para el modelo PCR |
| PCR_ANOVA | Conduce el análisis de la varianza (ANOVA) para el modelo PCR |
| PCR_FITTED | Calcula los valores de muestra ajustados (media, residuales) para el modelo PCR |
| PCR_FORE | Pronóstico (media, error y C.I) para el modelo PCR |
| PCR_PRTest | Prueba F parcial para PCR |
| PCR_STEPWISE | Realiza el método de selección paso a paso |
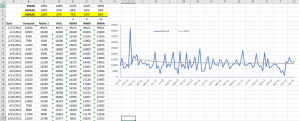
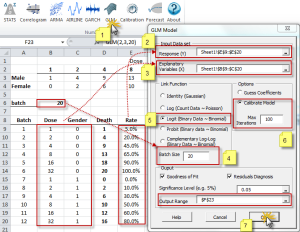
El Modelo lineal generalizado (GLM) es una generalización flexible de las regresiones cuadráticas menos ordinarias. El GLM generaliza una regresión lineal permitiendo que el modelo lineal se relacione con la variable de respuesta (i.e. $Y$) vía el vínculo de la función (i.e. $g(.)$) y permitiendo que la magnitud de la varianza de cada medida sea una función de su valor previsto.
El GLM se describe de la siguinete manera:
\[ Y = \mu + \epsilon \]
Y
\[ E\left[Y\right]=\mu=g^{-1}(X\beta) = g^{-1}(\eta) \]
Donde:
- $\epsilon$ es los residuos o la desviación con respecto a la media
- $g(.)$ es la función de enlace
- $g^{-1}(.)$ es la función inversa de vínculos o enlaces
- $X$ es la variable indeoendiente o factores exógenos
- $\beta$ es un vector de parámetros
- $\eta$ es elpredictor lineal: la cantidad que incorpora la información acerca de las variables independientes en el modelo.
$\eta=X\beta$
Funciones destacadas:
| Función | Descripción |
|---|---|
| GLM | Definición del modelo GLM |
| GLM_CHECK | Verifica los valores del modelo GLM |
| GLM_GUESS | Calcula un árido pero válido conjunto de valores de coeficientes para el modelo GLM dado |
| GLM_CALIBRATE | Calcula los valores de coeficientes del modelo optimizado de GLM (y errores) |
| GLM_LLF | Calcula la función logarítmica de verosimilitud (LLF) para el modelo GLM |
| GLM_MEAN | Calcula el valor interno de la muestra ajustado del modelo GLM |
| GLM_RESID | Calcula los términos de error/residuos en la muestra para el modelo GLM |
| GLM_FORE | Calcula la media de pronóstico del modelo GLM |
| GLM_FORECI | Intervalo de confianza de pronóstico GLM |
Ver también
En estadística, el análisis espectral es un procedimiento que deconstruye una serie de tiempo en un espectro de ciclos de diferentes longitudes. El análisis espectral se conoce también como análisis de dominio de frecuencia.
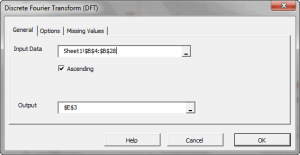
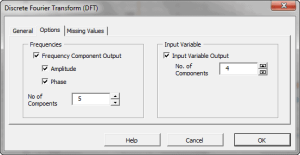
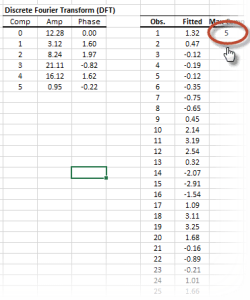
En principio, DFT convierte un discreto conjunto de observaciones en una serie de continuas funciones trigonométricas (ej. Seno y coseno). De manera que la señal original pueda ser representada como:
Where
- $k$ es el componente de frecuencia
- $x_0,…,x_{N-1}$ son los valores del ingreso de las series de tiempo
- $N$ es el número de valores no vacíos o faltantes e la entrtada de las series de tiempo
k \lt \frac{N}{2} \\ E_{\left (k-\frac{N}{2} \right )} – \ \alpha
\cdot O_{\left (k-\frac{N}{2} \right )} & \text{ if } k \geq
\frac{N}{2} \end{cases} \]
Where
- $E_k$ es la transformación discreta de Fourier (DFT) de los valores de los índices pares de las series de tiempo, $x_{2m} \left(x_0, x_2, \ldots, x_{N-2}\right)$
- $O_k$ es la transformación discreta de Fourier (DFT) de los valores de los índices impares de las series de tiempo, $x_{2m+1} \left(x_1, x_3, \ldots, x_{N-2}\right)$
- $\alpha = e^{ \left (-2 \pi i k /N \right )}$
- $N$ es el número de los valores no faltantes en los datos de las series de tiempo.
Funciones destacadas:
| Función | Descripción |
|---|---|
| DFT | Calcula la transformación discreta (rápida) de Fourier |
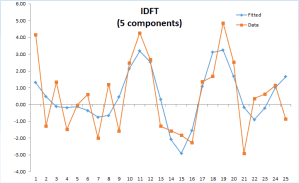
| IDFT | Calcula la inversa transformación discreta de Fourier |
Las funciones de los filtros deconstruyen las series de tiempo en tendencias y componentes cíclicos.
Funciones destacadas:
| Función | Descripción |
|---|---|
| NxBK | Aplica el filtro de Baxter-King |
| NxHP | Aplica el filtro de Hodrick Prescott |
| NxConv | Calcula la circunvolución del operador entre las dos series de tiempo. |
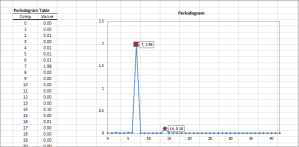
Un periodograma es un estimado de la densidad de poder espectral de una serie de tiempo. Este método es útil para identificar la estacionalidad dominante en el conjunto de datos subyacente.
Funciones destacadas:
| Función | Descripción |
|---|---|
| Periodogram | Calcula el valor estimado de la densidad espectral de potencia |
Ver también
- Videos Tutoriales
- Manual de Referencia
- Guía de Usuario
- Notas Técnicas
- Consejos y Trucoss
- Estudios de caso
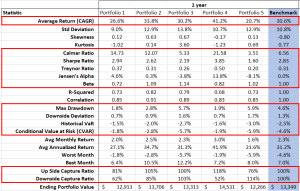
Analice la cartera para determinar la varianza y la covarianza de los rendimientos, simule la correlación de activos, calcule el valor en riesgo (VaR) de la cartera.
Regresión lineal simple (SLR)
Funciones destacadas:
| Función | Descripción |
|---|---|
| NxVaR | Arroja el valor de riesgo (VaR) histórico/teórico. |
| NxDWS | Devuelve la desviación a la baja de un conjunto de datos determinado. |
| NxCVaR | Devuelve el valor en riesgo condicional histórico/teórico (CVaR). |
| NxCAPM | Devuelve la versión beta del modelo de fijación de precios de activos de capital (CAPM). |
| NxCalmar | Devuelve la proporción Calmar. |
| NxSharpe | Develve la relación de Sharpe. |
| NxMCR | Devuelve el índice de captura del mercado al alza y a la baja. |
| NxJensen | Devuelve la medida alfa de Jensen en tasa de porcentaje anual (APR). |
| NxMDD | Devuelve la reducción máxima (MDD) en el conjunto de datos de serie temporal dado. |
| NxCAGR | Devuelve la tasa de crecimiento anual compuesta. |
| NxTreynor | Devuelve la relación de Treynor. |
Ver también
- Videos Tutoriales
- Manual de Referencia
- Guía de Usuario
- Notas Técnicas
- Consejos y Trucos
- Estudios de caso
En esta sección presentamos un conjunto de herramientas disponibles en la barra de herramientas de NumXL como un atajo para:
- calibrar los valores del modelo subyacente (ej.. ARMA, GARCH, GLM, etc,) usando el solucionador Microsft.
- Crear un modelo fuera de la muestra basado en el pronóstico,
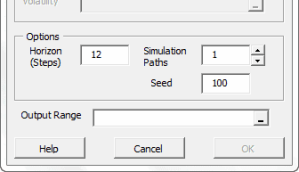
- ejecutar una simulación basada en el modelo
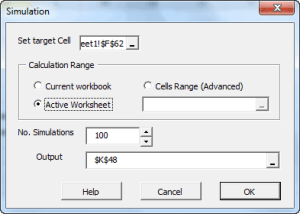
- Ejecución de la simulación de monte-carlo (MC)
Usando la celda activa actual, la herramienta de calibrado detecta el modelo subyacente, invoca y organiza los campos de solución de MS (ej. Función de utilidad, parámetros a ser optimizados, limitaciones, etc.) con cálculos en la tabla modelo seleccionada para el problema de optimización.
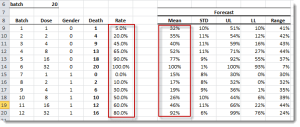
Usando la celda activa actual, la herramienta de pronóstico detecta un modelo subyacente, y exhibe la Interfaz de Usuario apropiada para las entradas recogidas requeridas (ej. Observación más reciente, horizonte de pronóstico, nivel de significancia, etc.) por el usuario final y, finalmente, genera una tabla de pronóstico con un apropiado C.I.
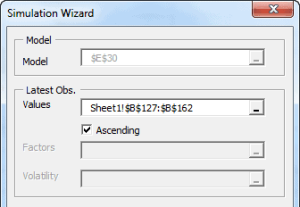
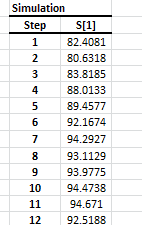
Usando la celda activa actual, la herramienta de simulación detecta el modelo designado y muestra la interfaz de usuario requerida para recoger entradas del usuario final (ej. Observaciones realizadas recientemente, horizonte, número de caminos de simulación, etc.) y generar caminos de simulación.
Esta funcionalidad es similar al concepto de tabla de datos de Excel, excepto porque no tiene valores de celdas predeterminados que calcular. En vez, asumiendo que tengamos una o más celdas con valores (ej. aleatorios) de volatilidad (y el resultado de nuestro(s) cálculo(s) esté afectado por esas celdas), la simulación de funcionalidad MC obliga a Excel a que re-calcule el rango de celdas/hojas de cálculo y capture los resultados de cada ejecución en un rango de celdas designado.
Ver también
- Videos Tutoriales
- Manual de Referencia
- Guía de Usuario
- Notas Técnicas
- Consejos y Trucos
- Estudios de caso
Una expresión regular (abreviada como regex) es una secuencia de caracteres que define la búsqueda de un patrón. El patrón puede ser aplicado así:
- (Emparejar) Hace coincidir un texto/cadena de textos, para un posible emparejamiento y, si se desea,
- (Extracto) Identifica y extrae una subcadena.
- (Reemplazar) Identifica y sustituye uno (o todos) los incidentes de una subcadena con otro valor
- (Tokenizar): Divide el texto en una serie de subcadenas, usando un patrón de separación dado.
Funciones destacadas:
| Función | Descripción |
|---|---|
| NxMatch | Función de emparejamiento de expresión regular (regex) |
| NxReplace | Función de reemplazo de expresión regular (regex) |
| NxTokenize | Separa una cadena mediante un delimitador en una matriz de subcadenas |
Detecta cualquier valor faltante en un conjunto de datos y eliminarlos si es posible.
Funciones destacadas:
| Función | Descripción |
|---|---|
| HASNA | Revisar la entrada de datos para observaciones con valores faltantes |
| RMNA | Remueve valores faltantes |
| MV_OBS | Número de observaciones con valores no faltantes |
| MV_VARS | Número efectivo de variables |
Las funciones en la categoría operan en una o dos celdas de datos dimensionales. Son muy útiles, especialmente cuando gestionamos valores faltantes, interpolación y/o al seleccionar un subgrupo de variables de entrada de datos.
Funciones destacadas:
| Función | Descripción |
|---|---|
| NxArray | Crea una matriz usando constantes y/o referencias de celda |
| NxFold | Convierte 3 columnas en una tabla 2-D o matriz |
| NxFlatten | Pliega una tabla de datos en una forma plana de 3 columnas |
| NxTranspose | Convierte una fila en columna (y viceversa) |
Instalación de NumXL e información de licencia del usuario.
Funciones destacadas:
| Función | Descripción |
|---|---|
| NUMXL_INFO | Recupera la información de instalación de NumXL |
Ver también
- Videos Tutoriales
- Manual de Referencia
- Guía de Usuario
- Notas Técnicas
- Consejos y Trucos
- Estudios de caso
Reseñas de clientes