Análisis de Tendencias para Datos de Series de Tiempo
No, no estamos hablando de la última tendencia en tecnología o moda; ¡Estamos hablando de análisis de tendencias para datos de series de tiempo! ¿Decepcionado? No lo esté, este es un tema emocionante y divertido.
En pocas palabras, las tendencias son la práctica de ajustar una curva a sus datos a lo largo del tiempo (por ejemplo, línea, polinomio, exponencial, etc.), en un esfuerzo por proyectar un pronóstico y establecer un intervalo de confianza.
¿Cómo se relaciona esto con el análisis de series de tiempo? Mientras que la curva de ajuste es una función del tiempo, los valores de los parámetros de la curva son calibrados (o ajustados) usando la información previa y por lo tanto están relacionados.
¿Por qué deberíamos preocuparnos?
La tendencia en Excel es comúnmente utilizada en la industria para hacer un pronóstico rápido. Los ejecutivos pueden utilizar la herramienta de tendencias como un ejercicio sano cuando examina resultados de modelos más avanzados.
En este artículo, revisaremos la tendencia en excel “NxTrend” Incorporado en la función que se introdujo por primera vez en NumXL 1.55 (LYNX) y demostraremos, a través de numerosos ejemplos, su uso y la intuición detrás de él. Nos vamos a concentrar en el aspecto de la prueba posterior y en el intervalo de confianza pronosticado.
Antecedentes
Microsoft Excel viene con una función incorporada “Tendencia”, pero se limita a tendencias lineales y no genera salidas distintas del valor ajustado. La función NxTrend empuja la aplicación de tendencia desde una línea agradable en un gráfico hasta un completo análisis de tendencias.
NxTrend soporta cinco (5) funciones de curva diferentes:
$$\begin{cases} \text{Linear} & a + b \times t \\ \text{Polynomial} & a + b_1 t+ b_2 t^2 + b_3 t^3 + \cdots + b_q t^q \\ \text{Exponential} & a \times e^{b \times t} \\ \text{Logarithm} & a + b \times \ln{t} \\ \text{Power} & a \times t^b \end{cases} $$
Cada una de las tendencias en las funciones de Excel soporta una intercepción fija (es decir, conocida) o flotación (es decir, calculada por el algoritmo de ajuste). También, las funciones de potencia y curva exponencial requieren que los valores de la serie de tiempo de muestra sean positivos.
Problema:
En la práctica, tenemos una muestra de datos tomada durante un período de tiempo. Tratamos de ajustar una curva paramétrica entre los puntos de tal manera que describa bien los datos y, una vez satisfechos, extenderemos la curva más allá del final de la muestra, pronosticando para puntos de datos futuros.
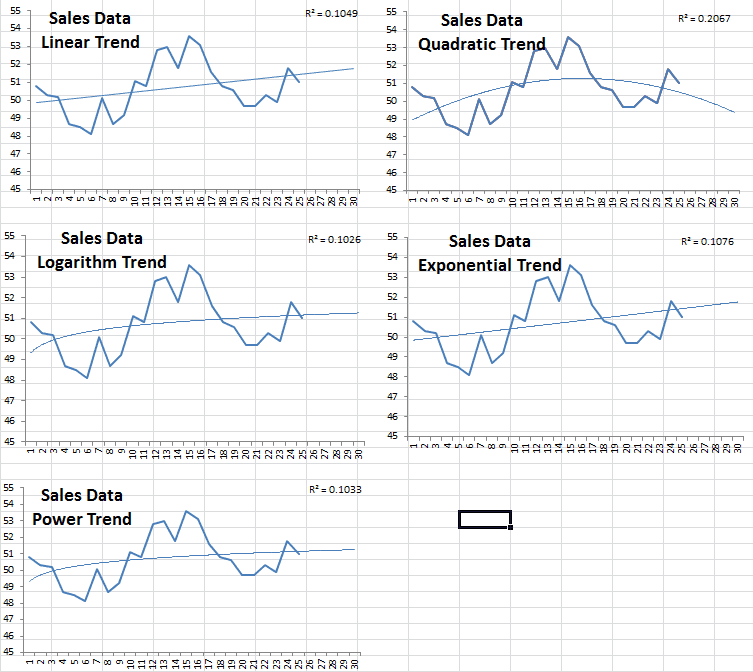
¿Interesante? Echemos un vistazo a un ejemplo de datos de ventas y utilice la característica de tendencia de Excel en gráficos:
Comparando las cinco curvas diferentes, la cuadrática tiene el R-cuadrado más alto, pero está proyectando que las ventas caigan después del mes 25, dicho esto, podemos decir definitivamente que preferiremos una de las otras cuatro posibilidades; Pero ¿cuál debería elegir?
Además, un pronóstico usualmente viene como un intervalo – de límites superiores e inferiores – con alguna medida de probabilidad para este rango. ¿Cómo podemos hacer eso con una curva de tendencia?
Solución:
Como practicante de análisis de datos o pronósticos, usted sabe que realizar pronósticos no es muy sencillo: usted necesita actualizar periódicamente su pronóstico a medida que se van realizando nuevos datos. Dicho esto, ¿cómo se ajustaría nuestra función de tendencia en el tiempo?
La descripción anterior se conoce como “prueba posterior”. Para nuestros propósitos aquí, queremos volver a probar la función de la tendencia.
- Vamos a ajustar el tiempo hacia atrás al comienzo de la muestra de datos más 2 (pocas observaciones acumuladas)
- Ejecutar la función de tendencia utilizando los datos anteriores
- Pronostique el valor actual y su intervalo de confianza – recuerde que retrocedimos en el tiempo.
- Mover el tiempo un paso adelante
- Repetir los pasos 2 y 4
Esto imita exactamente lo que usted haría al actualizar el pronóstico para incluir nuevas observaciones, por lo que hacer un backtesting le ayudará a ver cómo se ajustaría con diferentes curvas de tendencia.
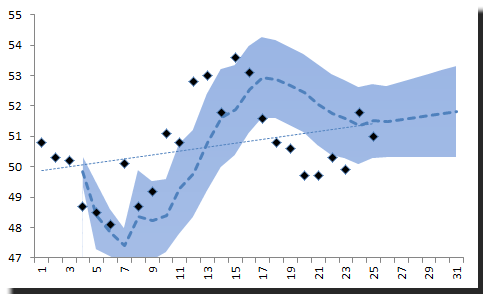
1) Tendencia lineal
Utilizando “NxTrend”, calculamos el pronóstico y su intervalo de confianza del 95% a lo largo de los datos de la muestra y los próximos 5 meses de pronóstico.
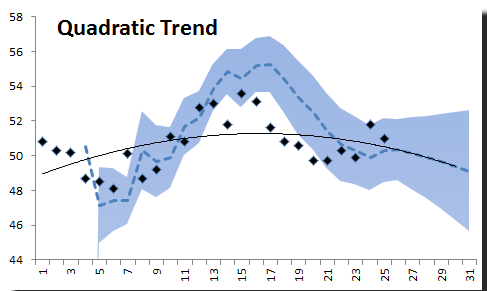
2) Tendencia cuadratica
Los polinomios de soporte de NxTrend de cualquier orden (suponiendo que tenga una muestra de datos de buen tamaño). Por lo tanto, para generar una curva de tendencia cuadrática, estableceremos el orden en 2.
La curva cuadrática de tendencia no se ve tan mal: pronostica una disminución en las ventas después del mes 24.Hay más puntos en el C.I. Que en la tendencia lineal que vimos antes.
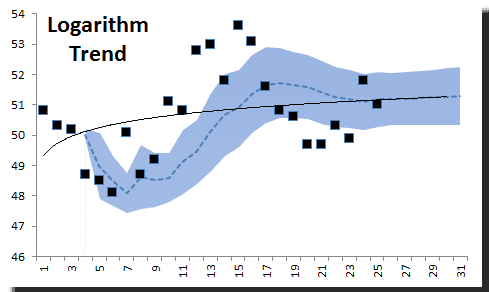
3) Tendencia logarítmica
Supongamos que los datos siguen el logaritmo del tiempo en lugar del tiempo en sí.
Obviamente, la tendencia logarítmica es inferior y no describe bien los datos. Vamos a desecharla, ponerla a un lado.
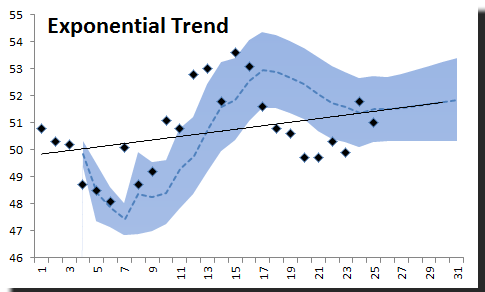
4) Tendencia Exponencial
Usando una tendencia exponencial en Excel, nos gustaría creer que nuestros datos crecen exponencialmente en el tiempo. Esto puede ser apropiado para algunos tipos de datos, como el crecimiento de la población.
La curva de tendencia exponencial parece estar bien en toda la muestra.
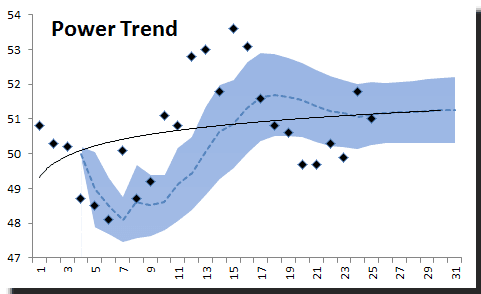
5) Power Trend
La tendencia de potencia, por otra parte, proporciona un ajuste muy pobre.
Conclusión
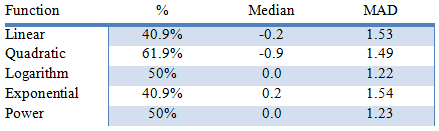
La pregunta más relevante ahora es: Que función de tendencia debo utilizar para mi pronóstico? Mi respuesta sería ninguna, pero si usted debe usar uno, tendríamos que llegar a una medida. Dado que estamos enfocados en la predicción, usaremos una medida para resumir los errores de pronóstico generados durante el backtesting.
- Relación entre el número de observaciones en la banda de intervalos de confianza
- Mediana – Medida robusta del centro de distribución de errores de pronóstico
- MAD – medida robusta de la dispersión del error de pronóstico
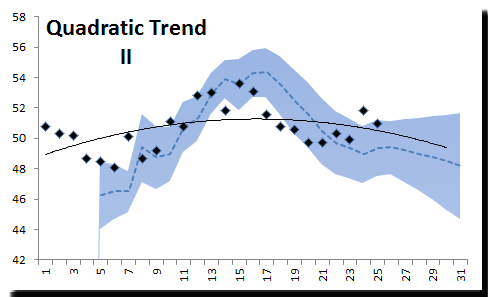
Una vez más, la función de tendencia cuadrática hizo lo mejor en nuestro análisis, pero su error de pronóstico tiene una mediana de 0,9 negativo. Para mejorar nuestros valores de pronóstico, podemos restar 0.9 a cualquier valor que nos proporcione la función de tendencia cuadrática. Aquí está el nuevo gráfico de tendencia cuadrática:
La línea punteada en la figura anterior corresponde al nuevo pronóstico (con 0.9 sustraído). La línea continua es la función de tendencia original.
Con esta modificación, 66.7% de los puntos están dentro de la banda del intervalo de confianza.