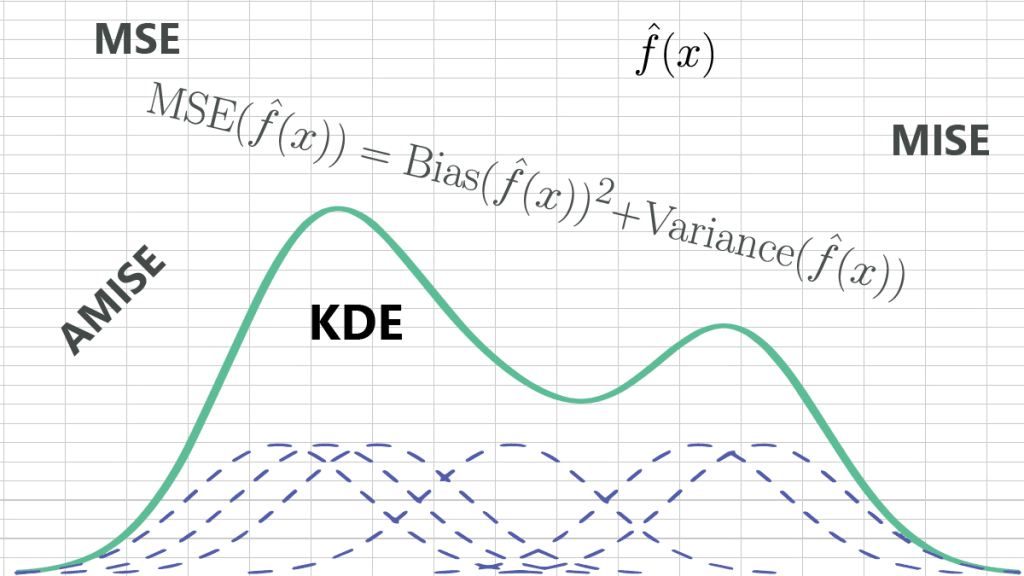
Introducción a la optimización de KDE
En estadística, la estimación de densidad kernel univariante (KDE) es una forma no paramétrica de estimar la función de densidad de probabilidad𝑓(𝑥) de una variable aleatoria X, un problema fundamental de suavizado de datos donde se hacen inferencias sobre la población, con base en una muestra finita de datos
Por qué usar la KDE?
Usando un núcleo en lugar de probabilidades discretas, promovemos la naturaleza de continuidad en la variable aleatoria subyacente.
Cómo calculamos la KDE?
En pocas palabras, colocamos una función de peso (también conocida como Kernel) en cada observación, y la función de densidad de probabilidad se expresa de la siguiente manera:
Donde:
- $k(.)$ es la función de Kernel.
- $h$ es el ancho de banda o el ancho de la ventana del núcleo.
- $N$ es el número de observaciones.
Para que el $\hat{f}\left(x\right)$ sea una función de probabilidad, la función kernel debe ser una función integrable, simétrica y no negativa hecha de valores reales.
Por tanto:
Cómo calcular el ancho de banda óptimo
Para una muestra de datos dada y una función de kernel, necesitamos un método consistente basado en datos para calcular el valor de ancho de banda óptimo.
¿Cómo determinamos la optimización de un núcleo (y ancho de banda) frente a otro? Primero necesitamos cuantificar la precisión de los estimadores kernel
Donde:
- $f(x)$ es la función de probabilidad subyacente (desconocida).
Expandamos la forma cuadrática:
Sume y reste el término de $2E\left(\hat{f}\left(x\right)\right)^2$, y re-ordene los términos:
Notas:
- El término $(\mathbb{E}(\hat{f}(x))-f(x))$ compara el valor de la densidad esperada con el actual. A este término se le llama “tendencia.”
- El segundo término es la varianza de la misma $\hat{f}(x)$ itself. $$\text{MSE}(\hat{f}(x))=\text{Bias}{{(\hat{f}(x))}^{2}}+\text{Variance}(\hat{f}(x))$$
Para todos los valores de $x\in (-\infty ,\infty )$, definimos el error cuadrático medio integrado (MISE):
Apliquemos la definición anterior a KDE:
- $\mathbb{E}(\hat{f}(x))$: $$\mathbb{E}(\hat{f}(x))=\frac{1}{n}\sum\limits_{i=1}^{n}{\mathbb{E}}(\frac{1}{h}K(\frac{x-{{X}_{i}}}{h}))$$ Asumiendo que $\{{{x}_{i}}\}$ sean independientes e identicamente distribuidas ($i.i.d$): $$\mathbb{E}(\hat{f}(x))=\frac{1}{n}\sum\limits_{i=1}^{n}{\frac{1}{h}}\int_{-\infty }^{\infty }{(K(}\frac{x-t}{h}))f(t)dt=\frac{1}{h}\int_{-\infty }^{\infty }{K}(\frac{x-t}{h})f(t)dt$$ $$\mathbb{E}(\hat{f}(x))=\frac{1}{h}\int_{-\infty }^{\infty }{K}(\frac{x-t}{h})f(t)dt=\frac{1}{h}\int_{-\infty }^{\infty }{h}K(z)f(x-hz).dz$$ Usando la expansión de Taylor: $$f(x-hz)=f(x)-hz{{f}^{(1)}}(x)+\frac{{{(hz)}^{2}}}{2}{{f}^{(2)}}(x)+O({{h}^{2}})$$ $$\mathbb{E}\left[ \hat{f}(x) \right]=\int_{-\infty }^{\infty }{K}(z)(f(x)-hz{{f}^{(1)}}(x)+\frac{{{(hz)}^{2}}}{2}{{f}^{(2)}}(x)).dz+O({{h}^{2}})$$ $$\mathbb{E}\left[ \hat{f}(x) \right]=f(x)+\text{ }\frac{{{h}^{2}}{{f}^{(2)}}(x)}{2}{{\mu }_{2}}(K)+O({{h}^{2}})$$ Donde ${{\mu }_{2}}(K)$ es el segundo momento de la función de kernel (i.e., ${{\mu }_{2}}(K)=\int_{-\infty }^{\infty }{{{z}^{2}}}K(z)dz$). De este modo, $\text{Bias}(\hat{f}(x))$ de la KDE se expresa así: $$\text{Bias}(\hat{f}(x))=\text{ }\frac{{{h}^{2}}{{f}^{(2)}}(x)}{2}{{\mu }_{2}}(K)+O({{h}^{2}})$$
- $\text{Var}(\hat{f}(x))$: Ahora, calculemos la varianza de la estimación de densidad: $$\text{Var}(\hat{f}(x))=\text{Var}\left( \frac{1}{nh}\sum\limits_{i=1}^{n}{K}(\frac{x-{{X}_{i}}}{h}) \right)$$ Asumiendo que $\{{{x}_{i}}\}$ sean independientes e identicamente distribuidas ($i.i.d$), los términos de covarianza son todos cero. $${\rm{Var}}(\hat f(x)) = {1 \over {{{(nh)}^2}}}\sum\limits_{i = 1}^n {{\rm{Var}}} \left( {K({{x – {X_i}} \over h})} \right)$$ Pero: $${\text{Var}}\left( {K(\frac{{x – t}}{h})} \right) = {\Bbb E}\left[ {K{{(\frac{{x – t}}{h})}^2}} \right] – {\Bbb E}{\left[ {K(\frac{{x – t}}{h})} \right]^2}$$ $${\rm{Var}}\left( {K({{x – t} \over h})} \right) = \int_{ – \infty }^\infty K {({{x – t} \over h})^2}f(t)dt – {\left[ {\int K ({{x – t} \over h}f(t)dt)} \right]^2}$$ Poniéndolo de nuevo en la ecuación anterior ${\rm{Var}}(\hat f(x))$: $${\rm{Var}}(\hat f(x)) = {1 \over {{{(nh)}^2}}}\sum\limits_{i = 1}^n {\int_{ – \infty }^\infty K } {({{x – t} \over h})^2}f(t)dt – {\left[ {\int K ({{x – t} \over h})f(t)dt)} \right]^2}$$ $${\rm{Var}}(\hat f(x)) = {1 \over {n{h^2}}}\left( {\int_{ – \infty }^\infty K {{({{x – t} \over h})}^2}f(t)dt – {{\left[ {\int K ({{x – t} \over h})f(t)dt)} \right]}^2}} \right)$$ Definamos $z = {{x – t} \over h}$: $${\rm{Var}}(\hat f(x)) = {1 \over {nh}}\int K {(z)^2}f(x – zh)dz – {1 \over n}{\left[ {\int K (z)f(x – zh)dz)} \right]^2}$$ Usando la expansión de Taylor: $${\rm{Var}}(\hat f(x)) = {1 \over {nh}}\int K {(z)^2}(f(x) – hz{f^{(1)}}(x) + {{{{(hz)}^2}} \over 2}{f^{(2)}}(x) + O({h^2}))dz – $$ $${1 \over n}{\left[ {\int K (z)(f(x) – hz{f^{(1)}}(x) + {{{{(hz)}^2}} \over 2}{f^{(2)}}(x) + O({h^2}))dz)} \right]^2}$$ $${\text{Var}}(\hat f(x)) = \frac{{f(x)R(K)}}{{nh}} + \frac{h}{{2n}}{f^{(2)}}(x)\int {{z^2}} K{(z)^2}dz – \frac{{{\Bbb E}{{[\hat f(x)]}^2}}}{n}$$ Donde: $$R(K) = \int K {(z)^2}dz$$ $${\text{Var}}(\hat f(x)) = \frac{{f(x)R(K)}}{{nh}} + \frac{{{\Bbb E}{{[\hat f(x)]}^2}}}{n}$$
- En conjunto, el error cuadrático medio (MSE) de KDE se calcula de la siguiente manera: $${\rm{MSE}}(\hat f(x)) = {\rm{Bias}}{(\hat f(x))^2} + {\rm{Variance}}(\hat f(x))$$ $${\text{MSE}}(\hat f(x)) = {\text{ }}\frac{{{h^4}{f^{(2)}}{{(x)}^2}\mu _2^2(K)}}{4} + \frac{{f(x)R(K)}}{{nh}} + \frac{{{\Bbb E}{{[\hat f(x)]}^2}}}{n} + O({h^2})$$ $${\rm{MSE}}(\hat f(x)) \approx {\rm{ }}{{{h^4}{f^{(2)}}{{(x)}^2}\mu _2^2(K)} \over 4} + {{f(x)R(K)} \over {nh}}$$
- Integrar sobre $x \in ( – \infty ,\infty )$ considerando solamente la parte dominante del MISE (asintótico): $${\rm{AMISE}}(\hat f(x)) \approx {\rm{ }}{{{h^4}\mu _2^2(K)R({f^{(2)}})} \over 4} + {{R(K)} \over {nh}}$$
Por favor note que AIMSE todavía tiene un término constante desconocido $R({f^{(2)}})$, que depende de la función de distribución de probabilidad verdadera subyacente desconocida:
Por ahora, supongamos que de alguna manera podemos estimar el término constante desconocido $R({f^{(2)}})$.
Tome la primera derivada de AIMSE y hágala igual a cero:
Re-ordene los términos:
Cuál Kernel debo usar?
Hay muchas funciones del núcleo que satisfacen las condiciones descritas anteriormente (por ejemplo, no negativas, simétricas, de valores reales e integrables) para elegir. Por ejemplo: Uniforme, triangular, gaussiano, bipeso, tripeso, Epanechnikov, coseno, etc.
En la fómula de ${\rm{AMISE}}({h_{{\rm{opt}}}})$ notamos el término $R{(K)^4} \times \mu _2^2(K)$, que depende solamente de la función de kernel $K$. ¿Cómo cuantificamos el efecto de la función kernel en el KDE óptimo?
Para responder a esta pregunta, primero definamos un nuevo término: eficiencia del núcleo. Utilizando el kernel de Epanechnikov como referencia, la eficiencia del kernel $K$ se define de la siguiente manera:
Sustituyendo la fórmula óptima de AIMSE:
Cuanto mayor sea la eficiencia, menor será el valor óptimo de AIMSE.
Examinemos la eficiencia de algunas funciones del núcleo:
| Kernel | ${\mu _2} = \int {{x^2}} K(x)dx$ | $R(K) = \int {{K^2}(x)dx} $ | ${\rm{Eff}}(K)$ |
|---|---|---|---|
| Epanechnikov | ${1 \over 5}$ | ${3 \over 5}$ | 100% |
| Uniforme | ${1 \over 3}$ | ${1 \over 2}$ | 92.95% |
| Triangular | ${1 \over 6}$ | ${2 \over 3}$ | 98.6% |
| Quartic (Biweight) | ${1 \over 7}$ | ${5 \over 7}$ | 99.4% |
| Triweight | ${1 \over 9}$ | ${{350} \over {429}}$ | 98.7% |
| Gaussiana | 1 | ${1 \over {2\sqrt \pi }}$ | 95.1% |
| Coseno | $1 - {8 \over {{\pi ^2}}}$ | ${{{\pi ^2}} \over {16}}$ | 99.9% |
¿Qué significan esos valores? Aunque el uso del kernel de Epanechnikov puede dar el AIMSE óptimo más bajo, la diferencia del AIMSE con otros kernels es relativamente pequeña.
Silverman (Regla de oro)
En el ancho de banda óptimo y la fórmula AIMSE, nos quedamos con un término desconocido: $R({f^{(2)}})$, que depende de la verdadera distribución de probabilidad desconocida, la misma función que estamos tratando de estimar con KDE.
¿Cómo hacemos para estimar esto? $R({f^{(2)}})$? L Supongamos que la distribución subyacente es gaussiana (i.e., $x \sim N(\mu ,{\sigma ^2})$). Esto se conoce como la regla general de Silverman.
La ${f^{(2)}}(x)$ se expresa así:
Sustituyendo en la fórmula de ancho de banda óptimo:
Donde:
- ${\sigma _{{\rm{IQR}}}}$ se define así: ${\sigma _{{\rm{IQR}}}} = {{Q3 – Q1} \over {{\Phi ^{ – 1}}(0.75) – {\Phi ^{ – 1}}(0.25)}} = {{Q3 – Q1} \over {1.34}}$
- ${\Phi ^{ – 1}}(.)$ es la función de distribución acumulada normal inversa.
Suponiendo que usamos una función kernel gaussiana ($R(K) = {1 \over {2\sqrt \pi }}$ y ${\mu _2}(K) = 1$), el ancho de banda óptimo se puede expresar de la siguiente manera:
Para funciones kernel no gaussianas, el ancho de banda óptimo se calcula de la siguiente manera:
| Kernel | ${h_{{\rm{opt}}}}$ |
|---|---|
| Uniforme | $\hat \sigma \times \root 5 \of {{{12\sqrt \pi } \over n}} = {{1.8431\hat \sigma } \over {\root 5 \of n }}$ |
| Triangular | $\hat \sigma \times \root 5 \of {{{64\sqrt \pi } \over n}} = {{2.576\hat \sigma } \over {\root 5 \of n }}$ |
| Quartic (Biweight) | $\hat \sigma \times \root 5 \of {{{280\sqrt \pi } \over {3n}}} = {{2.778\hat \sigma } \over {\root 5 \of n }}$ |
| Triweight | $\hat \sigma \times \root 5 \of {{{3150\sqrt \pi } \over {143n}}} = {{2.0812\hat \sigma } \over {\root 5 \of n }}$ |
| Epanechnikov | $\hat \sigma \times \root 5 \of {{{40\sqrt \pi } \over n}} = {{2.3449\hat \sigma } \over {\root 5 \of n }}$ |
| Coseno | $\hat \sigma \times \root 5 \of {{{{\pi ^6}\sqrt \pi } \over {6{{({\pi ^2} - 8)}^2}n}}} = {{2.4097\hat \sigma } \over {\root 5 \of n }}$ |
Aunque la suposición detrás de la regla empírica es bastante simplista, a menudo usamos este método como punto de partida para métodos de estimación de ancho de banda más sofisticados (por ejemplo, complemento directo).
Referencias
- Silverman, B.W. (1986). Density Estimation for Statistics and Data Analysis. Chapman & Hall/CRC London.
- W. Zucchini, Applied smoothing techniques, Part 1 Kernel Density Estimation., 2003
- Byeong U. Park and J. S. Marron. Comparison of Data-Driven Bandwidth Selectors. Journal of the American Statistical Association Vol. 85, No. 409 (Mar., 1990), pp. 66-72 (7 pages)