Promedio móvil ponderado (WMA)
Una media móvil se utiliza comúnmente con datos de series de tiempo para suavizar las fluctuaciones a corto plazo y resaltar tendencias o ciclos a largo plazo. Un promedio móvil ponderado tiene factores multiplicadores para dar diferentes ponderaciones a los datos en diferentes posiciones en la ventana de muestra.
$$Y_t=\frac{\sum_{i=1}^N{W_i X_{t-i}}}{\sum_{i=1}^N W_i}$$
- $W_i$ Es la i-ésima posición factor de peso is the i-th position weight-factor
- $\{X_t\}$ es la serie de tiempo original
- $\{Y_t\}$ es la serie de tiempo suavizada
- $Y_t$ utiliza los valores anteriores de N de las $X_t$ observacioness (es decir (i.e. $\{X_{t-1},X_{t-2},\cdots ,X_{t-N}\}$)
El promedio móvil ponderado tiene una ventana fija (es decir, N) y los factores se eligen típicamente para dar más peso a las observaciones recientes.
El tamaño de ventana (N) determina el número de puntos promediados en cada momento, por lo que un tamaño de ventanas más grande responde menos a los nuevos cambios en la serie temporal original y un tamaño de ventana pequeño puede hacer que la salida suavizada sea ruidosa.
- $\{w_i\}$ Factores de ponderación normalizados
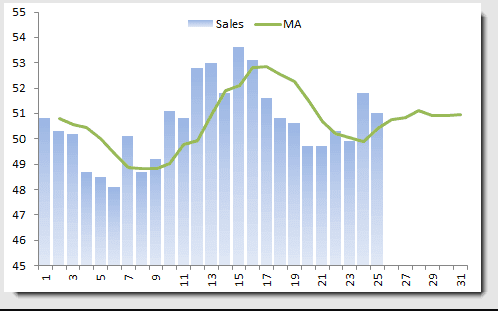
Consideremos las ventas mensuales de la Compañía X, usando una media móvil de 4 meses (de igual ponderación).
Tenga en cuenta que el promedio móvil está siempre rezagado detrás de los datos y que el pronóstico de la muestra converge a un valor constante.
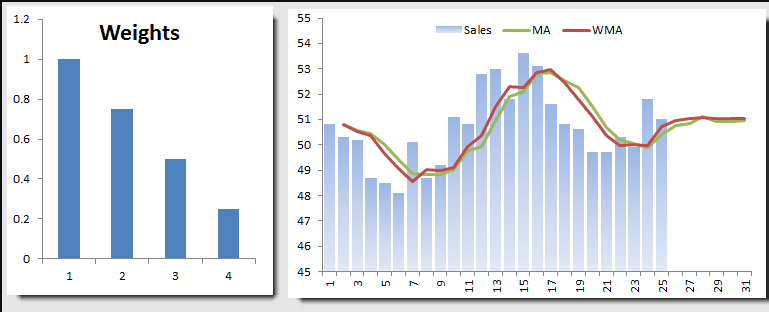
Tratemos de utilizar un esquema de ponderación (véase más adelante) que da más énfasis a la última observación.
Se graficó el promedio móvil ponderado igual y WMA en el mismo gráfico. El WMA parece más sensible a los cambios recientes y el pronóstico de fuera de la muestra converge al mismo valor que el promedio móvil.
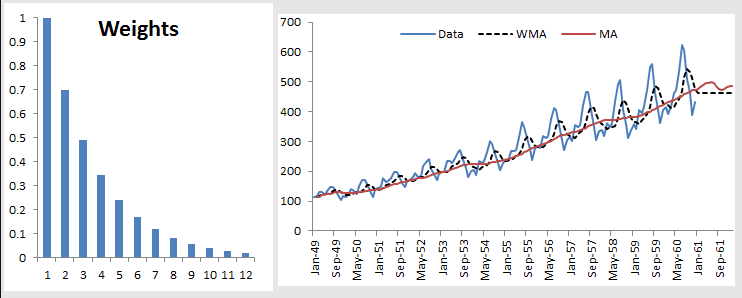
Examinemos la WMA en presencia de tendencia y estacionalidad. Para este ejemplo, utilizaremos los datos de la aerolínea internacional de pasajeros. La ventana del promedio móvil es de 12 meses.
El promedio móvil (MA) y promedio móvil ponderado (WMA) siguen el ritmo de la tendencia, pero el pronóstico de la muestra se aplana. Además, aunque el promedio móvil ponderado WMA exhibe alguna estacionalidad, siempre se queda atrás de los datos originales.