Holt’s Double Exponential Smoothing
Simple exponential smoothing does not do well in the presence of a trend, so several methods devised under the “Double Exponential” umbrella are proposed to handle this type of data.
NumXL supports Holt’s double exponential smoothing, which take the following formulation:
$$S_1=X_1$$ $$B_1=\frac{X_T-X_1}{T-1}$$ $$S_{t>1}=\alpha X_t + (1-\alpha)(S_{t-1}+B_{t-1})$$ $$B_{t>1}=\beta (S_t – S_{t-1})+(1-\beta)B_{t-1}$$ $$Y_t=\left\{\begin{matrix} S_t+B_t & t<T\\ S_T+m\times B_T & t=T+m \end{matrix}\right.$$
Where:
- $\alpha$ is the smoothing factor ($0 \prec \alpha \prec 1$)
- $\beta$ is the trend smoothing factor ($0 \prec \beta \prec 1$)
Example 1:
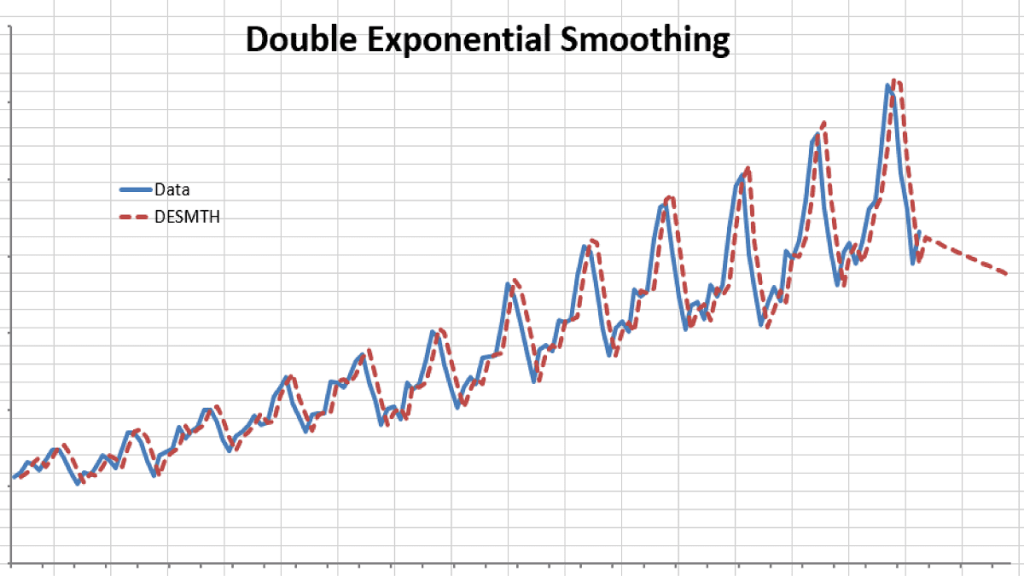
Let’s examine the international passengers’ airline data.
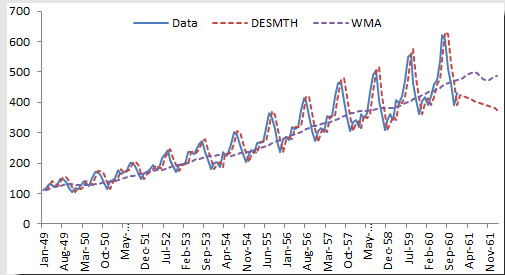
We chose an Alpha value of 0.9 and a Beta of 0.1. Please note that although double smoothing traces the original data well, the out-of-sample forecast is inferior to the simple moving average.
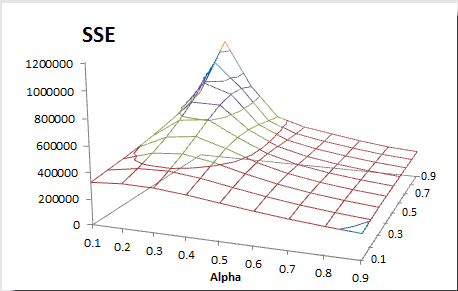
How do we find the best smoothing factors?
We take a similar approach to our simple exponential smoothing example but modified for two variables. We compute the sum of the squared errors; construct a two-variable data table, and pick the alpha and beta values that minimize the overall SSE.
Tutorial Video
Files Examples
Please click the button below to download Holt’s Double Exponential Smoothing example.