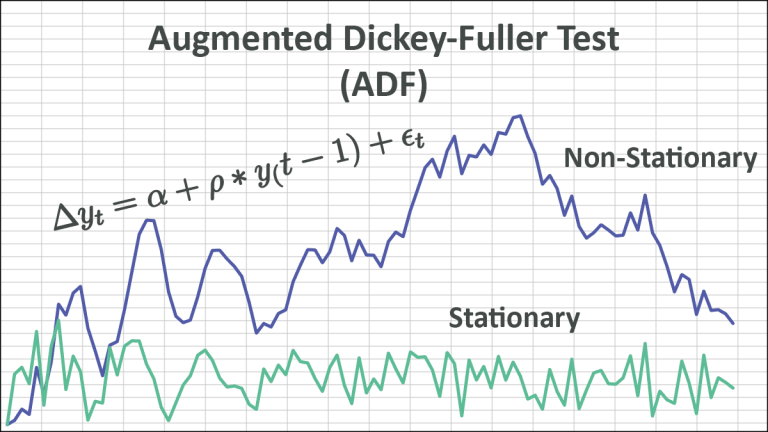
Augmented Dickey-Fuller (ADF)
Check out our latest Technical Notes article, an overview of stationarity and a deep dive into the DF and ADF tests
August 5, 2022
Menu
Read through the technical articles below related to NumXL features, functions, and applications.
Check out our latest Technical Notes article, an overview of stationarity and a deep dive into the DF and ADF tests
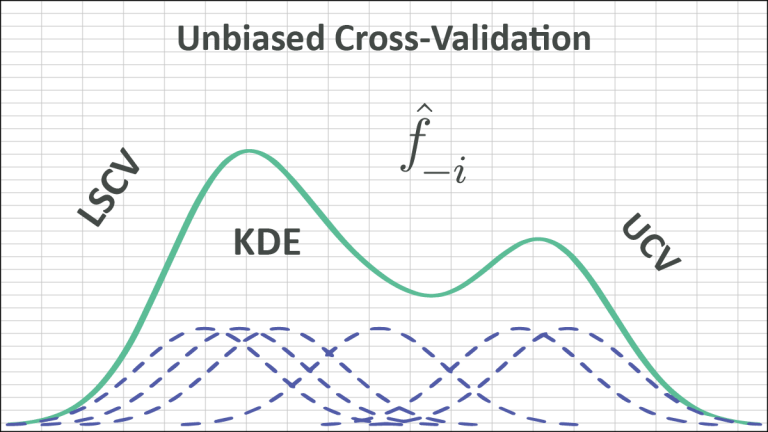
This paper introduces the unbiased cross-validation (UCV) optimization method, a popular data-based bandwidth selection for KDE.
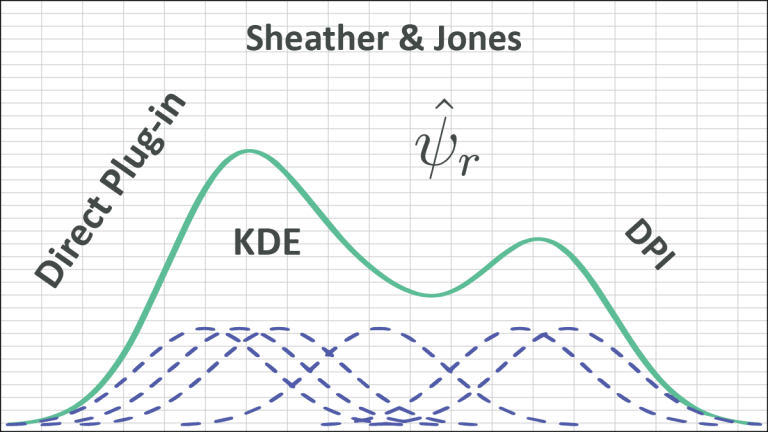
This paper introduces the Direct Plug-in, a popular KDE bandwidth calculation used for a broad set of cases.
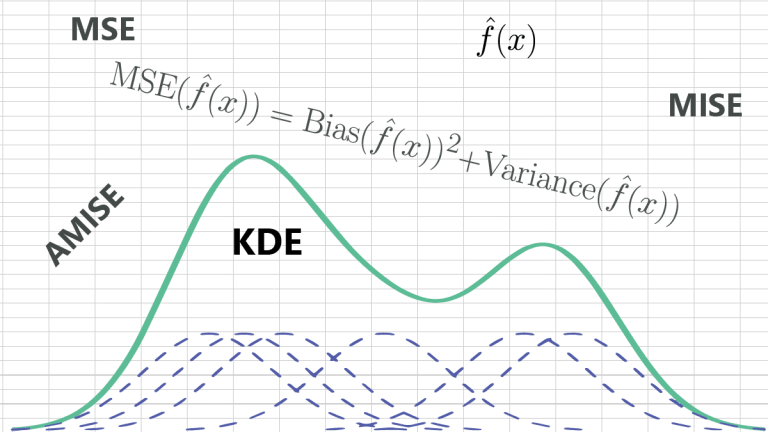
This article introduces the univariate kernel density estimation (KDE) method for estimating the probability density function of a random variable.
This article addresses the use of the Signal-to-Noise ratio (SNR) in a filter function and its application in a Low-Pass Filter.
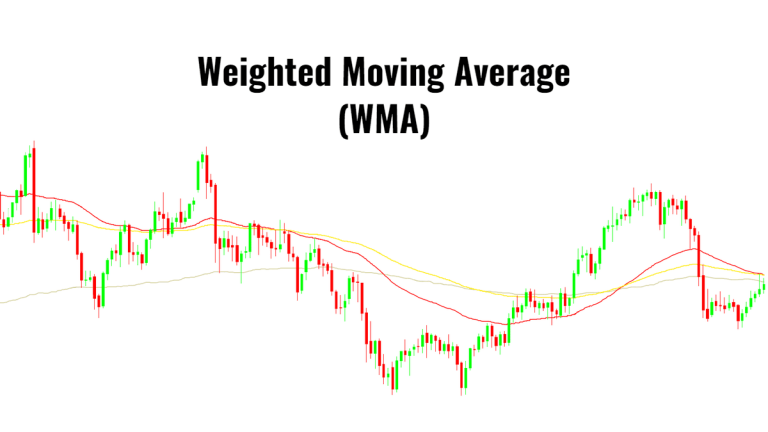
In this article, we will demonstrate the use of the WMA function in NumXL to smooth out time-series data and create a sample forecast.
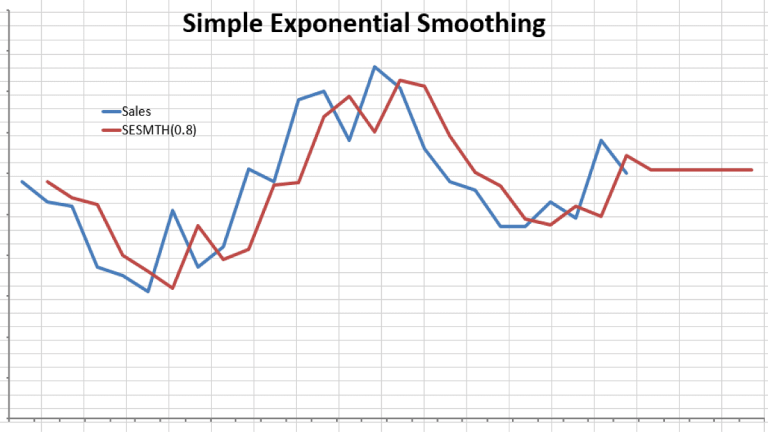
In this article, we’ll demonstrate some examples to show the Brown’s Simple Exponential Smoothing function in NumXL.
This article includes he data preparation aspect of time series analysis we start with the sampling assumptions of the time series.
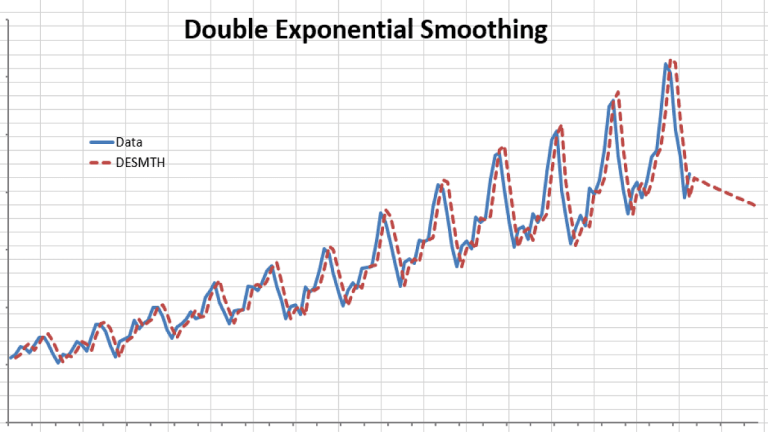
In this article, we’ll show some examples to demonstrate Holt’s Double Exponential Smoothing function.
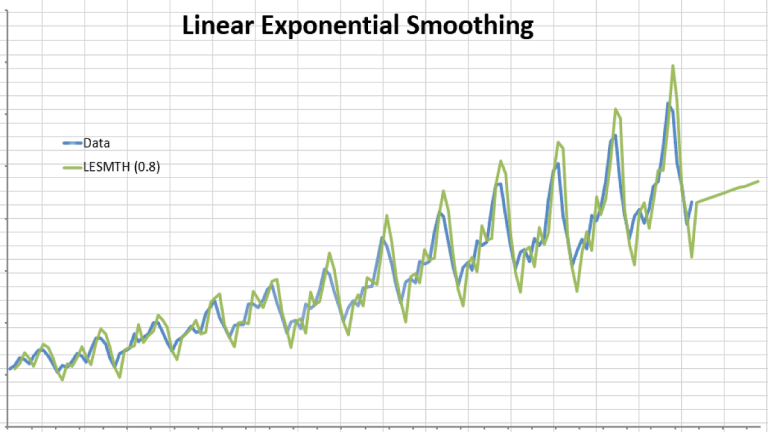
In this article, we’ll show some examples to demonstrate Brown’s Linear Exponential Smoothing function.
© 2023 Spider Financial Corp | | Terms & Conditions | Disclaimer | Privacy Policy | Trademarks & Copyrights
