Calculating Signal-to-Noise Ratio Using DFT
This article addresses the use of the Signal-to-Noise ratio (SNR) in a filter function and its application in a Low-Pass Filter.
September 22, 2020
Menu
Read through the articles related to the Discrete Fourier Transform (DFT) for time series.
The DFT is the most important discrete transform, used to perform Fourier analysis in many practical applications.
This article addresses the use of the Signal-to-Noise ratio (SNR) in a filter function and its application in a Low-Pass Filter.
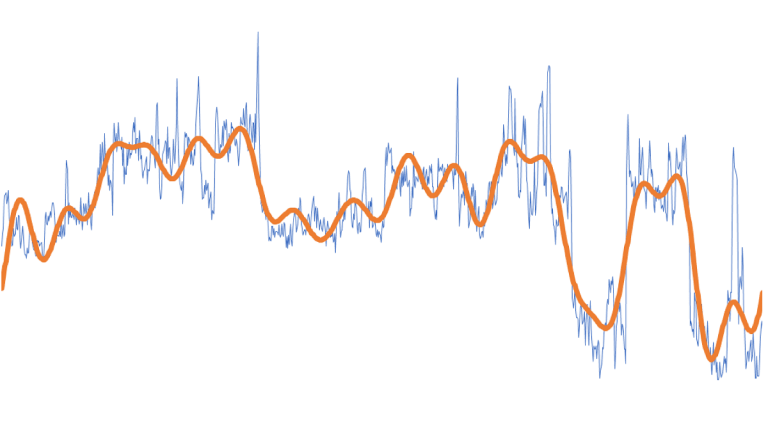
This issue addresses how to use Fourier Transform to filter a data signal using only K frequency components with the highest amplitudes.
This issue focuses on using the DFT components to represent the input data set as the sum of the trigonometric sine-cosine functions.
In this entry, we examine the Discrete Fourier Transform (DFT) and its inverse, as well as data filtering using DFT outputs.
© 2023 Spider Financial Corp | | Terms & Conditions | Disclaimer | Privacy Policy | Trademarks & Copyrights
