Brown’s Linear Exponential Smoothing
This is another method of double exponential smoothing function, but it has one smoothing factor:
$S_1^{‘}=X_1$
$S_1^{”}=X_1$
$S_{t>1}^{‘}=\alpha X_t + (1-\alpha)S_{t-1}^{‘}$
$S_{t>1}^{”}=\alpha S_{t}^{‘}+(1-\alpha)S_{t-1}^{”}$
$a_{1<t<T}=2
S_{t}^{‘}-S_t^{”}$
$b_{1<t<T}=\frac{\alpha}{1-\alpha}\times (S_t^{‘}-S_t^{”})$
$Y_{T+m}=a_T+m\times b_T$
Where:
- $\alpha$ is the smoothing factor ($0 \prec \alpha \prec 1$)
Brown’s double exponential smoothing takes one parameter less than Holt-Winter’s function, but it may not offer as good a fit as that function.
Example 1 :
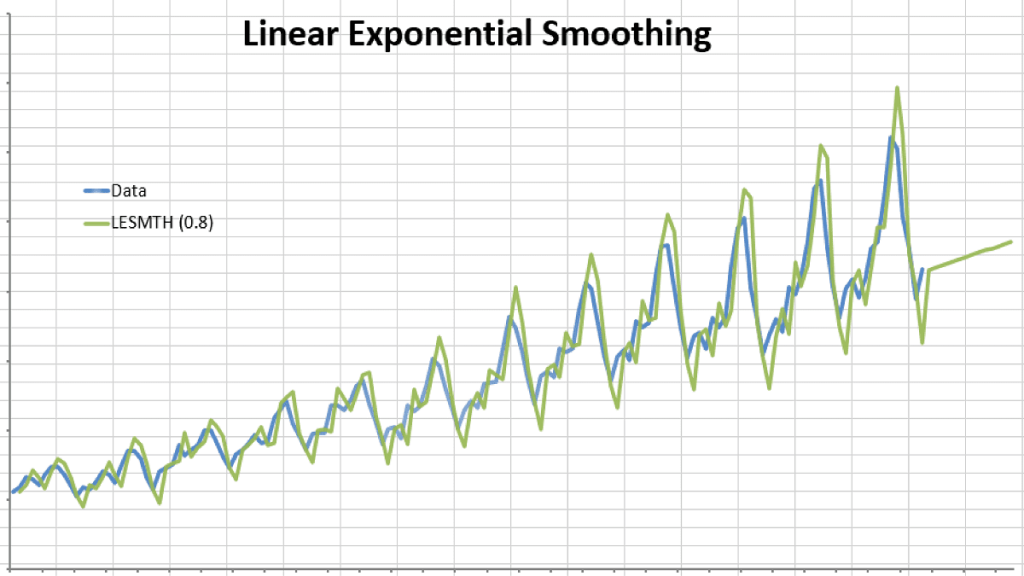
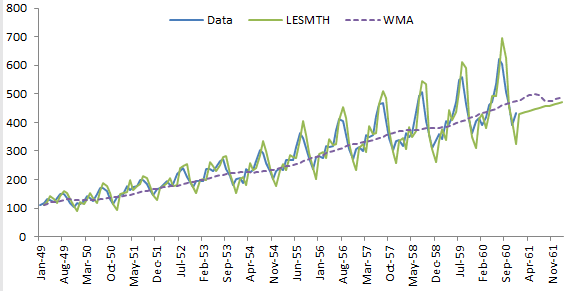
Let’s use the same example in Holt-Winter’s double exponential and compare the optimal sum of the squared error.
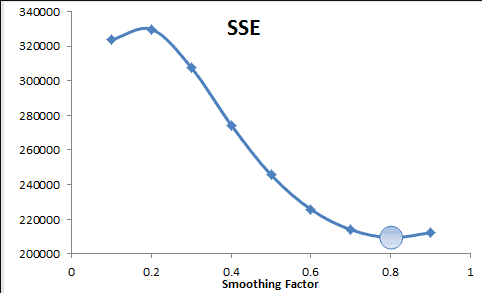
How do we find the best smoothing factor ($\alpha$)?
We use the same method to select the alpha value that minimizes the sum of the squared error. For the example sample data, the alpha is found to be 0.8
Tutorial Video
Files Examples
Please click the button below to download Brown’s Linear Exponential Smoothing example.