Holt-Winters’ Triple Exponential Smoothing
The triple exponential smoothing takes into account seasonal changes as well as trends. This method requires 4 parameters:
- $\alpha$: the smoothing factor
- $\beta$: the tend smoothing factor
- $\gamma$: the seasonality smoothing factor
- $\mathrm{L}$: the season Length
The formulation for triple exponential smoothing is more involved than any of
the earlier ones. Please, check our online reference manual for the exact formulation.
Example:
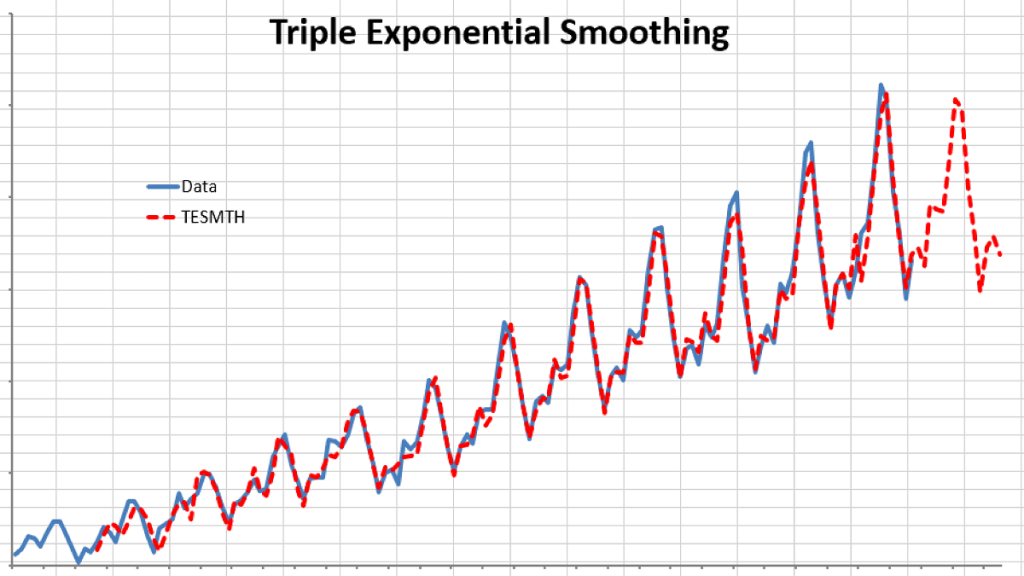
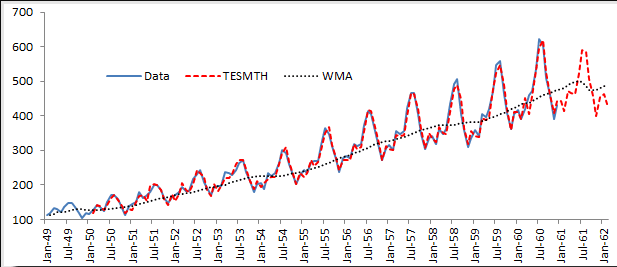
Using the international passengers’ airline data, we can apply winter’s triple
exponential smoothing, find optimal parameters, and conduct an out-of-sample
forecast.
Obviously, Winter’s triple exponential smoothing is best applied for this data sample, as it tracks the values well, and the out-of-sample forecast exhibits seasonality (L=12).
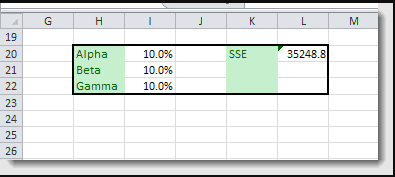
How do we find the best smoothing factor ($\alpha,\beta,\gamma$)?
Again, we need to pick the values that minimize the overall sum of the squared errors (SSE), but the data tables can be used for more than two variables, so we resort to the Excel solver:
(1) Setup the minimization problem, with the SSE as the utility function
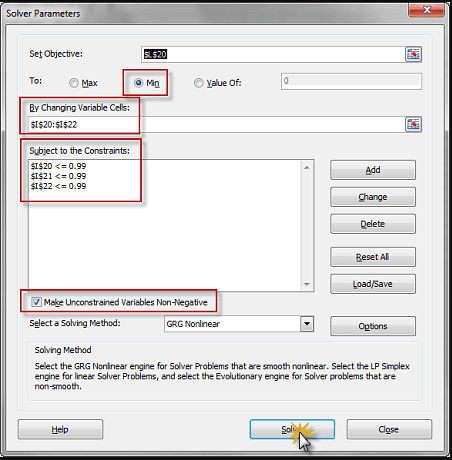
(2) The constraints for this problem
$$ 0 < \alpha < 1 $$ $$ 0 < \beta < 1 $$ $$ 0 < \gamma < 1 $$
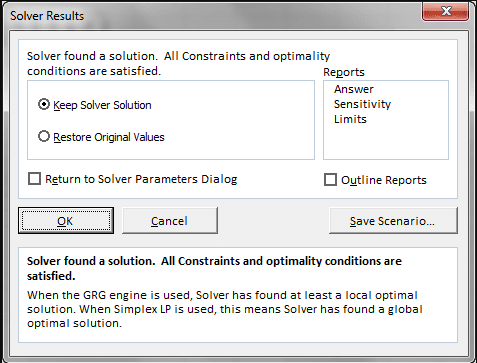
(3) Launch the Solver and initialize utility and constraints.
(4) The solver searches for the optimal solution, ultimately prompting its completion.
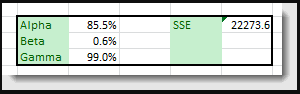
(5) The optimal values are:
Tutorial Video
Files Examples
Please click the button below to download Holt-Winters’ Triple Exponential Smoothing example.